Внутрипредметные связи
Применение геометрии в курсе алгебры
Часто при решении задач курса геометрии составляются уравнения, неравенства и их системы, затем они решаются. Таким образом, происходит так называемая алгебраизация геометрии.[1]
Алгебраизацией геометрии будем называть применение методов алгебры в решении геометрической задачи.Проникновение алгебры в геометрию, как правило, происходит на достаточно высоком уровне, т. е. осуществить алгебраизацию легко. А вот применение геометрии в алгебре в этом смысле отстаёт. Хотя ещё в 60-х годах вышла книга «Геометрия помогает арифметике» (Островский А. И., Кордемский Б. А.). Итак, можно также использовать геометрические соображения в задачах по алгебре.
Геометризация алгебры есть применение теории по геометрии в решении задач курса алгебры.|
Необходимо подчеркнуть, что применяется теория по геометрии только тогда, когда алгебраически решать крайне сложно или план решения задачи не ясен. Также основные темы по геометрии — это темы, которые изучаются школьниками в 7–9 классах. P. S. Книги и статьи, посвящённые геометризации, печатались уже в прошлом веке. |
Выявление внутрипредметных связей между геометрией и алгеброй, а также их взаимное проникновение друг в друга на уроках позволяет повторить и систематизировать знания обоих предметных областей.
Повторение приёмов работы с задачей
Напомним некоторые приёмы работы после решения сюжетной задачи.
Приёмы основываются на составлении:
Б) аналогичной задачи, т. е. происходит смена сюжета, но числовые данные не меняются;
В) другого способа решения задачи.Существуют задачи, которые можно решить и при помощи методов алгебры, и при использовании теории по геометрии.
Таблица внутрипредметных связей алгебры и начала анализа с геометрией
| Темы по алгебре и началам анализа | Теория по геометрии |
|---|---|
Вычисление значения алгебраического[2] выражения |
Подобные треугольники |
Тригонометрия: 1) формула косинуса разности 2) формула косинуса суммы 3) формула синуса разности 4) формула синуса суммы 5) доказательство тождеств 6) арк-функции (задачи на вычисление и доказательство) |
1) векторный метод[3]
2) решение треугольников 3) теорема Птолемея[4] 4) теорема Птолемея (но быстрее: метод площадей) 5) решение треугольников 6) решение треугольников |
Алгебраические уравнения, неравенства и их системы: 1] решение нелинейных систем уравнений 2] доказательство неравенств 3] решение иррациональных уравнений |
1] решение треугольников, векторный метод, координатный метод
2] векторный метод[5] 3] неравенство треугольника, метод „цепочки треугольников” |
Сюжетные задачи |
подобные треугольники (к теме: «Решение треугольников»), метод площадей |
Образцы оформления задач
Пример 1. Решение уравнения
Пример
Решить уравнение
Этап I. Выделение структуры задачи
Дано: , где .
Найти: , .
Этап II. Поиск решения, или анализ задачи
Особенности уравнения: оно иррациональное, а также содержит две переменные ( и ).
Решить уравнение сложно, попробуем подойти с геометрической точки зрения.
Этап III. Выбор метода решения задачи
Признаки выбора теории по геометрии: подкоренные выражения напоминают теорему косинусов[6].
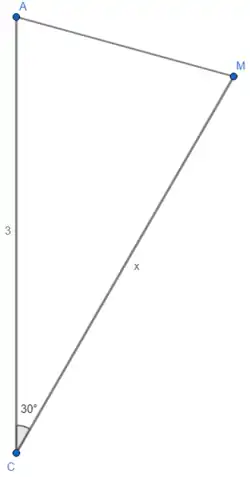
- Рассмотрим выражение . Оно равно , или, что то же самое, .
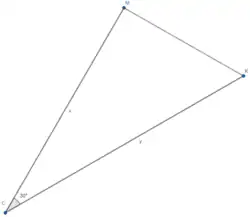
Итак, имеет место равенство . - Рассмотрим выражение . Оно равно , или, что то же самое, .
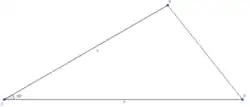
Итак, имеет место равенство . - Рассмотрим выражение . Оно равно , или, что то же самое, .
Итак, имеет место равенство .
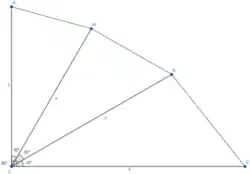
Теоретическая основа метода:
- метод „цепочки треугольников”
- тема: «Решение треугольников»
м
а
- ↑ Математика в школе. elib.mpgu.info. Дата обращения: 5 июня 2025.
- ↑ В основной школе под алгебраическим выражением понимается выражение из объединения семейств целых, дробно-рациональных и иррациональных выражений.
- ↑ Напомним, что вектор имеет две формы записи. Во-первых, вектор может рассматриваться как направленный отрезок (у некоторых авторов вектор отождествляется с параллельным переносом). А во-вторых, вектор может задаваться координатами.
- ↑ Во вписанном четырёхугольнике произведение диагоналей равно сумме произведений противоположных сторон.
- ↑ В данном случае вектор задаётся координатами.
- ↑ Формулировка: в треугольнике сумма квадратов двух сторон без их удвоенного произведения на косинус угла между ними равна квадрату третьей стороны.