Некоторые часто используемые формулы
Основные законы алгебры
Справедливы следующие тождества:
Переместительный (коммутативный) закон сложения:
a
+
b
=
b
+
a
.
{\displaystyle a+b=b+a.}
(Д1.1) Сочетательный (ассоциативный) закон сложения:
a
+
(
b
+
c
)
=
(
a
+
b
)
+
c
.
{\displaystyle a+(b+c)=(a+b)+c.}
(Д1.2) Переместительный (коммутативный) закон умножения:
a
⋅
b
=
b
⋅
a
.
{\displaystyle a\cdot b=b\cdot a.}
(Д1.3) Сочетательный (ассоциативный) закон умножения:
a
⋅
(
b
⋅
c
)
=
(
a
⋅
b
)
⋅
c
.
{\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c.}
(Д1.4) Распределительный (дистрибутивный) закон умножения относительно сложения:
a
⋅
(
b
+
c
)
=
a
⋅
b
+
a
⋅
c
.
{\displaystyle a\cdot (b+c)=a\cdot b+a\cdot c.}
(Д1.5)
Дроби
Здесь предполагается, что знаменатели дробей не обращаются в 0.
a
b
=
a
:
b
.
{\displaystyle {\frac {a}{b}}=a:b.}
(Д1.6)
a
b
=
a
c
b
c
=
a
:
c
b
:
c
.
{\displaystyle {\frac {a}{b}}={\frac {ac}{bc}}={\frac {a:c}{b:c}}.}
(Д1.7)
a
b
⋅
c
=
a
c
b
.
{\displaystyle {\frac {a}{b}}\cdot c={\frac {ac}{b}}.}
(Д1.8)
a
b
:
c
=
a
b
c
.
{\displaystyle {\frac {a}{b}}:c={\frac {a}{bc}}.}
(Д1.9)
a
b
±
c
d
=
a
d
±
b
c
b
d
.
{\displaystyle {\frac {a}{b}}\pm {\frac {c}{d}}={\frac {ad\pm bc}{bd}}.}
(Д1.10) В частности,
a
b
±
c
b
=
a
±
c
b
.
{\displaystyle {\frac {a}{b}}\pm {\frac {c}{b}}={\frac {a\pm c}{b}}.}
(Д1.11)
a
b
⋅
c
d
=
a
c
b
d
.
{\displaystyle {\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}.}
(Д1.12)
a
b
:
c
d
=
a
d
b
c
.
{\displaystyle {\frac {a}{b}}:{\frac {c}{d}}={\frac {ad}{bc}}.}
(Д1.13)
Пропорции
Из отношения, называемого пропорцией ,
a
b
=
c
d
{\displaystyle {\frac {a}{b}}={\frac {c}{d}}}
(Д1.14) следует, что
a
d
=
b
c
{\displaystyle ad=bc}
a
c
=
b
d
.
{\displaystyle {\frac {a}{c}}={\frac {b}{d}}.}
(Д1.15) Производные пропорции:
a
b
=
c
d
⇒
k
a
+
l
b
m
a
+
n
b
=
k
c
+
l
d
m
c
+
n
d
,
{\displaystyle {\frac {a}{b}}={\frac {c}{d}}\Rightarrow {\frac {ka+lb}{ma+nb}}={\frac {kc+ld}{mc+nd}},}
(Д1.16) где
m
,
n
{\displaystyle m,\;n}
m
a
+
n
b
≠
0
,
m
c
+
n
d
≠
0
{\displaystyle ma+nb\neq 0,\;mc+nd\neq 0}
В частности,
a
±
b
b
=
c
±
d
d
;
{\displaystyle {\frac {a\pm b}{b}}={\frac {c\pm d}{d}};}
(Д1.17)
a
±
b
a
∓
b
=
c
±
d
c
∓
d
.
{\displaystyle {\frac {a\pm b}{a\mp b}}={\frac {c\pm d}{c\mp d}}.}
(Д1.18) (Для правой и левой частей берутся либо только верхние знаки, либо только нижние.)
В общем:
a
1
b
1
=
a
2
b
2
=
…
=
a
n
b
n
⇒
k
1
a
1
+
k
2
a
2
+
…
+
k
n
a
n
k
1
b
1
+
k
2
b
2
+
…
+
k
n
b
n
.
{\displaystyle {\frac {a_{1}}{b_{1}}}={\frac {a_{2}}{b_{2}}}=\ldots ={\frac {a_{n}}{b_{n}}}\Rightarrow {\frac {k_{1}a_{1}+k_{2}a_{2}+\ldots +k_{n}a_{n}}{k_{1}b_{1}+k_{2}b_{2}+\ldots +k_{n}b_{n}}}.}
(Д1.19) В частности,
a
1
b
1
=
a
2
b
2
=
…
=
a
n
b
n
⇒
±
a
1
±
a
2
±
…
±
a
n
±
b
1
±
b
2
±
…
±
b
n
.
{\displaystyle {\frac {a_{1}}{b_{1}}}={\frac {a_{2}}{b_{2}}}=\ldots ={\frac {a_{n}}{b_{n}}}\Rightarrow {\frac {\pm a_{1}\pm a_{2}\pm \ldots \pm a_{n}}{\pm b_{1}\pm b_{2}\pm \ldots \pm b_{n}}}.}
(Д1.20) (Знаки в знаменателе должны повторять соответствующие знаки в числителе.)
Правила обращения со степенями
Предполагается, что операции допустимы.
a
α
⋅
a
β
=
a
α
+
β
.
{\displaystyle a^{\alpha }\cdot a^{\beta }=a^{\alpha +\beta }.}
(Д1.21)
a
α
a
β
=
a
α
−
β
.
{\displaystyle {\frac {a^{\alpha }}{a^{\beta }}}=a^{\alpha -\beta }.}
(Д1.22)
(
a
α
)
β
=
a
α
⋅
β
.
{\displaystyle (a^{\alpha })^{\beta }=a^{\alpha \cdot \beta }.}
(Д1.23)
(
a
⋅
b
)
α
=
a
α
⋅
b
α
.
{\displaystyle (a\cdot b)^{\alpha }=a^{\alpha }\cdot b^{\alpha }.}
(Д1.24)
(
a
b
)
α
=
a
α
b
α
.
{\displaystyle \left({\frac {a}{b}}\right)^{\alpha }={\frac {a^{\alpha }}{b^{\alpha }}}.}
(Д1.25) Считается, что
1
α
=
1
,
0
α
=
0
{\displaystyle 1^{\alpha }=1,\quad 0^{\alpha }=0}
0
0
{\displaystyle 0^{0}}
неопределено !),
a
1
=
a
,
a
0
=
1
,
a
−
1
=
1
a
(
a
≠
0
)
;
{\displaystyle a^{1}=a,\quad a^{0}=1,\quad a^{-1}={\frac {1}{a}}\;(a\neq 0);}
(Д1.26)
a
+
∞
=
{
+
∞
,
a
>
1
;
0
,
0
<
a
<
1
;
a
−
∞
=
{
0
,
a
>
1
;
+
∞
,
0
<
a
<
1.
{\displaystyle a^{+\infty }={\begin{cases}+\infty ,&a>1;\\0,&0<a<1;\end{cases}}\quad a^{-\infty }={\begin{cases}0,&a>1;\\+\infty ,&0<a<1.\end{cases}}}
(Д1.27)
Тождества сокращённого умножения
Бином Ньютона:
(
a
+
b
)
n
=
a
n
+
C
n
1
a
n
−
1
b
+
C
n
2
a
n
−
2
b
2
+
…
+
C
n
k
a
n
−
k
b
k
+
…
+
b
n
=
∑
m
=
0
n
(
n
m
)
a
n
−
m
b
m
,
{\displaystyle (a+b)^{n}=a^{n}+C_{n}^{1}a^{n-1}b+C_{n}^{2}a^{n-2}b^{2}+\ldots +C_{n}^{k}a^{n-k}b^{k}+\ldots +b^{n}=\sum _{m=0}^{n}{\binom {n}{m}}a^{n-m}b^{m},}
(Д1.28)
Рисунок Д1.1. Первые 5 строк треугольника Паскаля.где
C
n
m
=
(
n
m
)
=
n
!
m
!
(
n
−
m
)
!
{\displaystyle C_{n}^{m}={\binom {n}{m}}={\frac {n!}{m!(n-m)!}}}
n
{\displaystyle n}
m
{\displaystyle m}
биномиальные коэффициенты ;
n
!
=
1
⋅
2
⋅
3
⋅
…
⋅
n
{\displaystyle n!=1\cdot 2\cdot 3\cdot \ldots \cdot n}
n
{\displaystyle n}
0
!
=
1
{\displaystyle 0!=1}
Для степени разности будем иметь:
(
a
−
b
)
n
=
a
n
−
C
n
1
a
n
−
1
b
+
C
n
2
a
n
−
2
b
2
−
…
+
(
−
1
)
k
C
n
k
a
n
−
k
b
k
+
…
+
(
−
1
)
n
b
n
.
{\displaystyle (a-b)^{n}=a^{n}-C_{n}^{1}a^{n-1}b+C_{n}^{2}a^{n-2}b^{2}-\ldots +(-1)^{k}C_{n}^{k}a^{n-k}b^{k}+\ldots +(-1)^{n}b^{n}.}
(Д1.29) Числа
C
n
m
{\displaystyle C_{n}^{m}}
треугольник Паскаля рисунка Д1.1
Частные случаи формул (Д1.28 ) и (Д1.29 ):
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}
(Д1.30)
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}}
(Д1.31)
(
a
+
b
)
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}}
(Д1.32)
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}}
(Д1.33)
(
a
+
b
)
4
=
a
4
+
4
a
3
b
+
6
a
2
b
2
+
4
a
b
3
+
b
4
{\displaystyle (a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}}
(Д1.34)
(
a
−
b
)
4
=
a
4
−
4
a
3
b
+
6
a
2
b
2
−
4
a
b
3
+
b
4
{\displaystyle (a-b)^{4}=a^{4}-4a^{3}b+6a^{2}b^{2}-4ab^{3}+b^{4}}
(Д1.35) Формулу бинома можно обобщить на случай, так называемых мультиномов :
(
a
+
b
+
…
+
c
)
n
=
∑
k
1
,
k
2
,
…
,
k
m
⩾
0
,
k
1
+
k
2
+
…
+
k
m
=
n
(
n
k
1
,
k
2
,
…
,
k
m
)
a
k
1
b
k
2
…
c
k
m
,
{\displaystyle (a+b+\ldots +c)^{n}=\sum _{\begin{smallmatrix}k_{1},\;k_{2},\;\ldots ,\;k_{m}\geqslant 0,\\k_{1}+k_{2}+\ldots +k_{m}=n\end{smallmatrix}}{\binom {n}{k_{1},\;k_{2},\;\ldots ,\;k_{m}}}a^{k_{1}}b^{k_{2}}\ldots c^{k_{m}},}
(Д1.36) где
(
n
k
1
,
k
2
,
…
,
k
m
)
=
n
!
k
1
!
k
2
!
…
k
m
!
{\displaystyle {\binom {n}{k_{1},\;k_{2},\;\ldots ,\;k_{m}}}={\frac {n!}{k_{1}!k_{2}!\ldots k_{m}!}}}
обобщённые биномиальные коэффициенты , или мультиномиальные коэффициенты
В частности,
(
a
+
b
+
c
)
3
=
a
3
+
b
3
+
c
3
+
3
a
2
b
+
3
a
2
c
+
3
b
2
a
+
3
b
2
c
+
3
c
2
a
+
3
c
2
b
+
6
a
b
c
.
{\displaystyle (a+b+c)^{3}=a^{3}+b^{3}+c^{3}+3a^{2}b+3a^{2}c+3b^{2}a+3b^{2}c+3c^{2}a+3c^{2}b+6abc.}
(Д1.37) При
n
=
3
{\displaystyle n=3}
триномиальные ») образуют пирамиду Паскаля .
Исходя из правил деления многочленов, можно получить следующие формулы для алгебраической суммы степеней:
a
n
−
b
n
=
(
a
−
b
)
(
a
n
−
1
+
a
n
−
2
b
+
…
+
a
b
n
−
2
+
b
n
−
1
)
;
{\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+\ldots +ab^{n-2}+b^{n-1});}
(Д1.38)
a
2
k
+
1
+
b
2
k
+
1
=
(
a
+
b
)
(
a
2
k
−
a
2
k
−
1
b
+
a
2
k
−
2
b
2
−
…
−
a
b
2
k
−
1
+
b
2
k
)
.
{\displaystyle a^{2k+1}+b^{2k+1}=(a+b)(a^{2k}-a^{2k-1}b+a^{2k-2}b^{2}-\ldots -ab^{2k-1}+b^{2k}).}
(Д1.39)
a
2
k
−
b
2
k
=
(
a
−
b
)
(
a
2
k
−
1
+
a
2
k
−
2
b
+
a
2
k
−
3
b
2
+
…
+
a
b
2
k
−
2
+
b
2
k
−
1
)
;
{\displaystyle a^{2k}-b^{2k}=(a-b)(a^{2k-1}+a^{2k-2}b+a^{2k-3}b^{2}+\ldots +ab^{2k-2}+b^{2k-1});}
(Д1.40) В частности,
a
2
−
b
2
=
(
a
−
b
)
(
a
+
b
)
{\displaystyle a^{2}-b^{2}=(a-b)(a+b)}
(Д1.41)
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}
(Д1.42)
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})}
(Д1.43)
a
4
−
b
4
=
(
a
+
b
)
(
a
3
−
a
2
b
+
a
b
2
−
b
3
)
=
(
a
+
b
)
(
a
−
b
)
(
a
2
+
b
2
)
{\displaystyle a^{4}-b^{4}=(a+b)(a^{3}-a^{2}b+ab^{2}-b^{3})=(a+b)(a-b)(a^{2}+b^{2})}
(Д1.44)
Средние величины
A
=
x
1
+
x
2
+
…
+
x
n
n
.
{\displaystyle A={\frac {x_{1}+x_{2}+\ldots +x_{n}}{n}}.}
(Д1.45)
V
=
a
1
x
1
+
a
2
x
2
+
…
+
a
n
x
n
a
1
+
a
2
+
…
+
a
n
,
{\displaystyle V={\frac {a_{1}x_{1}+a_{2}x_{2}+\ldots +a_{n}x_{n}}{a_{1}+a_{2}+\ldots +a_{n}}},}
(Д1.46) где
a
1
+
a
2
+
…
+
a
n
≠
0
{\displaystyle a_{1}+a_{2}+\ldots +a_{n}\neq 0}
Среднее арифметическое является частным случаем среднего взвешенного при
a
1
=
a
2
=
…
=
a
n
=
1
{\displaystyle a_{1}=a_{2}=\ldots =a_{n}=1}
G
=
x
1
⋅
x
2
⋅
…
⋅
x
n
n
=
(
x
1
⋅
x
2
⋅
…
⋅
x
n
)
1
n
,
{\displaystyle G={\sqrt[{n}]{x_{1}\cdot x_{2}\cdot \ldots \cdot x_{n}}}=(x_{1}\cdot x_{2}\cdot \ldots \cdot x_{n})^{\frac {1}{n}},}
(Д1.47) где
x
1
⩾
0
,
x
2
⩾
0
,
…
,
x
n
⩾
0
{\displaystyle x_{1}\geqslant 0,\;x_{2}\geqslant 0,\;\ldots ,\;x_{n}\geqslant 0}
Среднее взвешенное геометрическое:
S
=
(
x
1
a
1
⋅
x
2
a
2
⋅
…
⋅
x
n
a
n
)
1
s
,
{\displaystyle S=(x_{1}^{a_{1}}\cdot x_{2}^{a_{2}}\cdot \ldots \cdot x_{n}^{a_{n}})^{\frac {1}{s}},}
(Д1.48) где
x
1
⩾
0
,
x
2
⩾
0
,
…
,
x
n
⩾
0
{\displaystyle x_{1}\geqslant 0,\;x_{2}\geqslant 0,\;\ldots ,\;x_{n}\geqslant 0}
s
=
a
1
+
a
2
+
…
+
a
n
{\displaystyle s=a_{1}+a_{2}+\ldots +a_{n}}
Среднее геометрическое является частным случаем среднего взвешенного геометричесокго при
a
1
=
a
2
=
…
=
a
n
=
1
{\displaystyle a_{1}=a_{2}=\ldots =a_{n}=1}
H
=
n
1
x
1
+
1
x
2
+
…
+
1
x
n
.
{\displaystyle H={\frac {n}{{\dfrac {1}{x_{1}}}+{\dfrac {1}{x_{2}}}+\ldots +{\dfrac {1}{x_{n}}}}}.}
(Д1.49)
K
=
x
1
2
+
x
2
2
+
…
+
x
n
2
n
.
{\displaystyle K={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\ldots +x_{n}^{2}}{n}}}.}
(Д1.50) Имеет место следующее неравенство (неравенство Коши ):
n
1
x
1
+
1
x
2
+
…
+
1
x
n
⩽
x
1
⋅
x
2
⋅
…
⋅
x
n
n
⩽
x
1
+
x
2
+
…
+
x
n
n
.
{\displaystyle {\frac {n}{{\dfrac {1}{x_{1}}}+{\dfrac {1}{x_{2}}}+\ldots +{\dfrac {1}{x_{n}}}}}\leqslant {\sqrt[{n}]{x_{1}\cdot x_{2}\cdot \ldots \cdot x_{n}}}\leqslant {\frac {x_{1}+x_{2}+\ldots +x_{n}}{n}}.}
(Д1.51)
Абсолютная величина
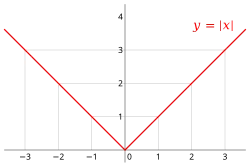
Рисунок Д1.2. График функции
y
=
|
x
|
{\displaystyle \scriptstyle {y=|x|}}
Абсолютной величиной , или модулем
|
x
|
{\displaystyle |x|}
кусочно-линейная функция (рисунок Д1.2
|
x
|
=
{
x
,
x
⩾
0
;
−
x
,
x
<
0.
{\displaystyle |x|={\begin{cases}x,&x\geqslant 0;\\-x,&x<0.\end{cases}}}
(Д1.52) Альтернативное определение:
|
x
|
=
max
{
x
,
−
x
}
.
{\displaystyle |x|=\max\{x,\;-x\}.}
(Д1.53) Модулем комплексного числа
z
=
x
+
y
i
{\displaystyle z=x+yi}
|
z
|
=
|
x
+
y
i
|
=
(
R
e
z
)
2
+
(
I
m
z
)
2
=
x
2
+
y
2
.
{\displaystyle |z|=|x+yi|={\sqrt {(\mathrm {Re} \,z)^{2}+(\mathrm {Im} \,z)^{2}}}={\sqrt {x^{2}+y^{2}}}.}
(Д1.53)
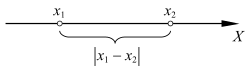
Рисунок Д1.3. Геометрическая интерпретация модуля.Геометрически (рисунок Д1.3
|
x
1
−
x
2
|
{\displaystyle |x_{1}-x_{2}|}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
|
x
|
{\displaystyle |x|}
вещественной прямой с координатами
x
{\displaystyle x}
O
{\displaystyle O}
Свойства
|
x
|
⩾
0
{\displaystyle |x|\geqslant 0}
|
x
|
=
0
{\displaystyle |x|=0}
x
=
0
{\displaystyle x=0}
(Д1.54)
|
x
⋅
y
|
=
|
x
|
⋅
|
y
|
.
{\displaystyle |x\cdot y|=|x|\cdot |y|.}
(Д1.55)
|
x
y
|
=
|
x
|
|
y
|
,
y
≠
0.
{\displaystyle \left|{\frac {x}{y}}\right|={\frac {|x|}{|y|}},\quad y\neq 0.}
(Д1.56) Если существует
x
α
{\displaystyle x^{\alpha }}
|
x
α
|
=
|
x
|
α
.
{\displaystyle |x^{\alpha }|=|x|^{\alpha }.}
(Д1.57)
x
2
k
2
k
=
|
x
|
.
{\displaystyle {\sqrt[{2k}]{x^{2k}}}=|x|.}
(Д1.58)
−
x
2
k
+
1
=
−
|
x
|
2
k
+
1
.
{\displaystyle {\sqrt[{2k+1}]{-x}}=-{\sqrt[{2k+1}]{|x|}}.}
(Д1.59)
|
x
+
y
|
⩽
|
x
|
+
|
y
|
{\displaystyle |x+y|\leqslant |x|+|y|}
неравенство треугольника .(Д1.60) Имеет место и более общее свойство:
|
x
+
y
+
…
+
z
|
⩽
|
x
|
+
|
y
|
+
…
+
|
z
|
{\displaystyle |x+y+\ldots +z|\leqslant |x|+|y|+\ldots +|z|}
|
∑
i
=
1
m
x
i
|
⩽
∑
i
=
1
m
|
x
i
|
.
{\displaystyle \left|\sum _{i=1}^{m}x_{i}\right|\leqslant \sum _{i=1}^{m}|x_{i}|.}
(Д1.61)
|
|
x
|
−
|
y
|
|
⩽
|
x
−
y
|
{\displaystyle ||x|-|y||\leqslant |x-y|}
(Д1.62)
Методы уничтожения иррациональности
В некоторых задачах часто возникает потребность избавится от иррациональности в числителе или знаменателе в выражении вида
P
Q
{\displaystyle {\frac {P}{Q}}}
P
{\displaystyle P}
Q
{\displaystyle Q}
Основным методом уничтожения иррациональности является метод умножения на сопряжённый множитель.
Сопряжённым множителем относительно выражения
S
{\displaystyle S}
K
≢
0
{\displaystyle K\not \equiv 0}
S
⋅
K
{\displaystyle S\cdot K}
S
=
X
p
Y
q
⋅
…
⋅
Z
l
n
,
{\displaystyle S={\sqrt[{n}]{X^{p}Y^{q}\cdot \ldots \cdot Z^{l}}},}
(Д1.63) где
p
,
q
,
…
,
l
,
n
∈
N
{\displaystyle p,\;q,\;\ldots ,\;l,\;n\in \mathbb {N} }
p
,
q
,
…
,
l
<
n
{\displaystyle p,\;q,\;\ldots ,\;l<n}
K
=
X
n
−
p
Y
n
−
q
⋅
…
⋅
Z
n
−
l
n
.
{\displaystyle K={\sqrt[{n}]{X^{n-p}Y^{n-q}\cdot \ldots \cdot Z^{n-l}}}.}
(Д1.64) Действительно, домножив
S
{\displaystyle S}
K
{\displaystyle K}
S
⋅
K
=
X
⋅
Y
⋅
…
⋅
Z
.
{\displaystyle S\cdot K=X\cdot Y\cdot \ldots \cdot Z.}
(Д1.65)
S
=
X
n
±
Y
n
{\displaystyle S={\sqrt[{n}]{X}}\pm {\sqrt[{n}]{Y}}}
(Д1.66) сопряжённый множитель находится, исходя из формул (Д1.38 )—(Д1.40 ).
Для выражения
S
=
X
n
−
Y
n
{\displaystyle S={\sqrt[{n}]{X}}-{\sqrt[{n}]{Y}}}
(Д1.67) сопряжённый множитель
K
=
X
n
−
1
n
+
X
n
−
2
⋅
Y
n
+
…
+
X
⋅
Y
n
−
2
n
+
Y
n
−
1
n
.
{\displaystyle K={\sqrt[{n}]{X^{n-1}}}+{\sqrt[{n}]{X^{n-2}\cdot Y}}+\ldots +{\sqrt[{n}]{X\cdot Y^{n-2}}}+{\sqrt[{n}]{Y^{n-1}}}.}
(Д1.68) Для выражения
S
=
X
2
k
+
Y
2
k
{\displaystyle S={\sqrt[{2k}]{X}}+{\sqrt[{2k}]{Y}}}
(Д1.69) сопряжённый множитель
K
=
X
2
k
−
1
2
k
−
X
2
k
−
2
⋅
Y
2
k
+
…
+
X
⋅
Y
2
k
−
2
2
k
−
Y
2
k
−
1
2
k
.
{\displaystyle K={\sqrt[{2k}]{X^{2k-1}}}-{\sqrt[{2k}]{X^{2k-2}\cdot Y}}+\ldots +{\sqrt[{2k}]{X\cdot Y^{2k-2}}}-{\sqrt[{2k}]{Y^{2k-1}}}.}
(Д1.70) Для выражения
S
=
X
2
k
+
1
+
Y
2
k
+
1
{\displaystyle S={\sqrt[{2k+1}]{X}}+{\sqrt[{2k+1}]{Y}}}
(Д1.71) сопряжённый множитель
K
=
X
2
k
2
k
+
1
−
X
2
k
−
1
⋅
Y
2
k
+
1
+
…
−
X
⋅
Y
2
k
−
1
2
k
+
1
+
Y
2
k
2
k
+
1
.
{\displaystyle K={\sqrt[{2k+1}]{X^{2k}}}-{\sqrt[{2k+1}]{X^{2k-1}\cdot Y}}+\ldots -{\sqrt[{2k+1}]{X\cdot Y^{2k-1}}}+{\sqrt[{2k+1}]{Y^{2k}}}.}
(Д1.72) В частности, для выражения
S
=
X
±
Y
{\displaystyle S={\sqrt {X}}\pm {\sqrt {Y}}}
(Д1.73) сопряжённый множитель равен:
K
=
X
∓
Y
,
{\displaystyle K={\sqrt {X}}\mp {\sqrt {Y}},}
(Д1.74) а для выражения
S
=
X
3
±
Y
3
{\displaystyle S={\sqrt[{3}]{X}}\pm {\sqrt[{3}]{Y}}}
(Д1.75) имеет вид:
K
=
X
2
3
∓
X
⋅
Y
3
+
Y
2
3
.
{\displaystyle K={\sqrt[{3}]{X^{2}}}\mp {\sqrt[{3}]{X\cdot Y}}+{\sqrt[{3}]{Y^{2}}}.}
(Д1.76) Сопряжённый множитель для выражений вида
S
=
X
n
±
Y
m
,
{\displaystyle S={\sqrt[{n}]{X}}\pm {\sqrt[{m}]{Y}},}
(Д1.77) где
n
≠
m
{\displaystyle n\neq m}
S
=
X
p
k
±
Y
s
k
,
{\displaystyle S={\sqrt[{k}]{X^{p}}}\pm {\sqrt[{k}]{Y^{s}}},}
(Д1.78) где
k
{\displaystyle k}
наименьшее общее кратное (НОК) чисел
m
{\displaystyle m}
n
{\displaystyle n}
p
=
k
n
,
s
=
k
m
{\displaystyle p={\frac {k}{n}},\;s={\frac {k}{m}}}
Также для преобразований бывает полезна формула сложного радикала:
A
±
B
=
A
+
A
2
−
B
2
±
A
−
A
2
−
B
2
,
{\displaystyle {\sqrt {A\pm {\sqrt {B}}}}={\sqrt {\frac {A+{\sqrt {A^{2}-B}}}{2}}}\pm {\sqrt {\frac {A-{\sqrt {A^{2}-B}}}{2}}},}
(Д1.79) где
A
⩾
0
,
B
⩾
0
,
A
2
⩾
B
{\displaystyle A\geqslant 0,\;B\geqslant 0,\;A^{2}\geqslant B}
При преобразовании радикалов важно помнить, что:
X
2
k
2
k
=
|
X
|
;
{\displaystyle {\sqrt[{2k}]{X^{2k}}}=|X|;}
(Д1.80)
−
X
2
k
+
1
=
−
|
X
|
2
k
+
1
.
{\displaystyle {\sqrt[{2k+1}]{-X}}=-{\sqrt[{2k+1}]{|X|}}.}
(Д1.81)