Основы теоретической физики/Кеплерова задача

Наиболее важным для практических применений случаем центральных полей, является поле с потенциальной энергией

${\displaystyle U\sim {\frac {1}{r}}}$ (1.4.36)

К полям такого типа относятся гравитационные и кулоновские. Частицы в этих полях могут испытывать на себе силы притяжения и отталкивания:

${\displaystyle F\sim {\frac {1}{r^{2}}}}$ (1.4.37)

Введем коэффициент пропорциональности в   (1.4.36)    и рассмотрим вначале поле притяжения:

${\displaystyle \left\{{\begin{aligned}&U=-{\frac {\alpha }{r}}\\&\alpha >0\\\end{aligned}}\right.}$ (1.4.38)

Из-за того, что потенциальная энергия отрицательна, полная энергия тоже может быть меньше нуля. Эффективная потенциальная энергия из   (1.4.31)   :

${\displaystyle U_{\text{эф}}=-{\frac {\alpha }{r}}+{\frac {M^{2}}{2m{r^{2}}}}}$ (1.4.39)

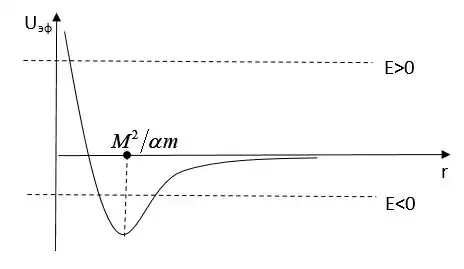
Функция   (1.4.39)    имеет минимум:

${\displaystyle {\begin{aligned}&r_{\min }={\frac {M^{2}}{\alpha m}}\\&{{\left(U_{\text{эф}}\right)}_{\min }}=-{\frac {\alpha m}{2{M^{2}}}}\\\end{aligned}}}$ (1.4.40)

Из графика функции ${\displaystyle U_{\text{эф}}(r)}$ видно, что если полная энергия частицы больше нуля (E>0), движение будет инфинитным, а при E<0 движение финитное.

Если подставить   (1.4.38)    в   (1.4.29)   , то можно взять интеграл и получить траекторию частицы в явном виде как функцию ${\displaystyle \varphi (r)}$:

${\displaystyle \varphi (r)=\arccos {\frac {\displaystyle {\frac {M}{r}}-{\frac {m\alpha }{M}}}{\sqrt {2mE+{\frac {{m^{2}}{\alpha ^{2}}}{M^{2}}}}}}+const}$ (1.4.41)

Для большей наглядности, если рассматривать случай финитного движения при E<0, выражение   (1.4.41)    можно преобразовать, выбрав начало отсчета таким, чтобы константа равнялась нулю и вводя новые обозначения:

${\displaystyle {\begin{aligned}&p={\frac {M^{2}}{m\alpha }}\\&e={\sqrt {1+{\frac {2E{M^{2}}}{m{{\alpha }^{2}}}}}}\\\end{aligned}}}$ (1.4.42)

Подставляя   (1.4.42)    в   (1.4.41)   , получим уравнение траектории в виде:

${\displaystyle {\frac {p}{r}}=1+e\cos \varphi }$ (1.4.43)

Полученное выражение   (1.4.43)    – это уравнение конического сечения (эллипса) с фокусом в начале координат. То есть величины «p» и «e» в   (1.4.43)    это «параметр» и «эксцентриситет» эллиптической орбиты. Сделанный выбор начала координат означает, что точка с углом ${\displaystyle \varphi =0}$ - является ближайшей к центру. Эта точка называется «перигелий» орбиты.

Ранее мы показали, что задача двух тел может быть сведена к задаче движения одного тела. Значит в случае двух тел, орбита тоже представляет собой коническое сечение с фокусом в их общем центре инерции.

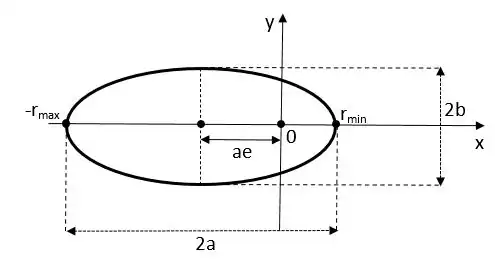
Из   (1.4.42)    понятно, что если энергия E<0, то эксцентриситет e<1, то есть в этом случае орбита будет эллиптической. Большая и малая полуоси эллипса могут быть найдены по формулам:

${\displaystyle {\begin{aligned}&a={\frac {p}{1-e^{2}}}={\frac {\alpha }{2{\big \vert }E{\big \vert }}}\\&b={\frac {p}{\sqrt {1-e^{2}}}}={\frac {M}{\sqrt {2m{\big \vert }E{\big \vert }}}}\\\end{aligned}}}$ (1.4.44)

Также можно найти наименьшее и наибольшее расстояния до центра поля (до фокуса эллипса в точке 0):

${\displaystyle {\begin{aligned}&{r_{\min }}={\frac {p}{1+e}}=a(1-e)\\&{r_{\max }}={\frac {p}{1-e}}=a(1+e)\\\end{aligned}}}$ (1.4.45)

Эллипс переходит в окружность если эксцентриситет e=0. Значит энергия тела, движущегося по круговой орбите, находится по формуле:

${\displaystyle E=-{\frac {\alpha m}{2M^{2}}}={{\left(U_{\text{эф}}\right)}_{\min }}}$ (1.4.46)

Время обращения по орбите (период) можно определить из второго закон Кеплера   (1.4.25)    если известна площадь орбиты (эллипса):

${\displaystyle \left.{\begin{aligned}&2m{\frac {S}{T}}=M\\&S=\pi ab\\\end{aligned}}\right\}\Rightarrow T={\frac {2\pi mab}{M}}=\pi \alpha {\sqrt {\frac {m}{2E^{3}}}}}$ (1.4.47)

Формула   (1.4.47)    показывает, что период в данном случае, зависит только от полной энергии частицы.

В случае инфинитного движения при ${\displaystyle E\geq 0}$, эксцентриситет e>1, значит траектория будет гиперболой, огибающей центр поля.

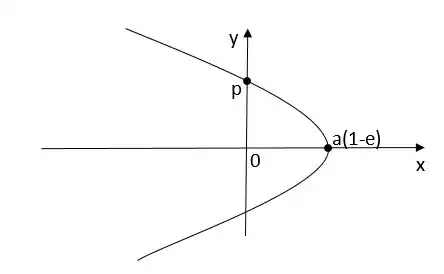
Выбрав начало отсчета таким, чтобы константа в   (1.4.41)    равнялась нулю и используя обозначения   (1.4.42)   , получим формулы для полуоси гиперболы и для расстояния перигелия от центра:

${\displaystyle {\begin{aligned}&a={\frac {p}{e^{2}-1}}={\frac {\alpha }{2E}}\\&{r_{\min }}={\frac {p}{e+1}}=a(e-1)\\\end{aligned}}}$ (1.4.48)

В случае если E=0, e=1, траекторией является парабола. Этот случай осуществляется, когда движение частицы начинается из состояния покоя на бесконечности.

<<Назад  |  Далее>>
Оглавление