Основы теоретической физики/Одномерное движение

По определению, одномерным называют движение с одной степенью свободы. Функцию Лагранжа системы с одной степенью свободы, запишем пользуясь общей формулой   (1.1.51)   :

${\displaystyle L={\frac {1}{2}}a(q){{\dot {q}}^{2}}-U(q)}$ (1.4.1)

Или для декартовых координат можно записать:

${\displaystyle L={\frac {1}{2}}m{{\dot {x}}^{2}}-U(x)}$ (1.4.2)

Подставим функцию   (1.4.2)    в уравнения движения   (1.1.24)   . Для одной степени свободы получаем:

${\displaystyle {\begin{aligned}&{\frac {d}{dt}}{\frac {\partial }{\partial {\dot {x}}}}\left({\frac {1}{2}}m{{\dot {x}}^{2}}-U(x)\right)-{\frac {\partial }{\partial x}}\left({\frac {1}{2}}m{{\dot {x}}^{2}}-U(x)\right)=0\\&{\frac {d}{dt}}\left(m{\dot {x}}\right)-{\frac {\partial U}{\partial x}}=0\\&m{\ddot {x}}-{\frac {\partial U}{\partial x}}=0\\\end{aligned}}}$ (1.4.3)

Чтобы найти теперь траекторию, нужно решить уравнение   (1.4.3)   . Для решения нужно знать конкретный вид потенциальной энергии U(x). Если эта функция не известна, то в общем виде траекторию и время движения удобней искать с помощью закона сохранения энергии:

${\displaystyle {\frac {1}{2}}m{{\dot {x}}^{2}}+U(x)=E=const}$ (1.4.4)

Найдем теперь из   (1.4.4)    в общем виде траекторию и время движения:

${\displaystyle {\begin{matrix}\displaystyle {\frac {dx}{dt}}={\sqrt {{\frac {2}{m}}\left(E-U\right)}}\\\Downarrow \\\displaystyle {\begin{aligned}&x={\sqrt {\frac {2}{m}}}\int \limits _{t_{1}}^{t_{2}}{dt{\sqrt {E-U(x)}}}\\&t={\sqrt {\frac {m}{2}}}\int \limits _{x_{1}}^{x_{2}}{\frac {dx}{\sqrt {E-U(x)}}}\\\end{aligned}}\\\end{matrix}}}$ (1.4.5)

В формуле   (1.4.5)    подкоренное выражение должно быть больше нуля. Физически это означает, что движение возможно только если кинетическая энергия больше нуля:

${\displaystyle \left.{\begin{aligned}&E-U(x)>0\\&E=T+U\\\end{aligned}}\right\}\Rightarrow {\begin{aligned}&T+U-U>0\\&T>0\\\end{aligned}}}$ (1.4.6)

Области энергий, при которых возможно или невозможно движение, можно изобразить на графике зависимости U(x).

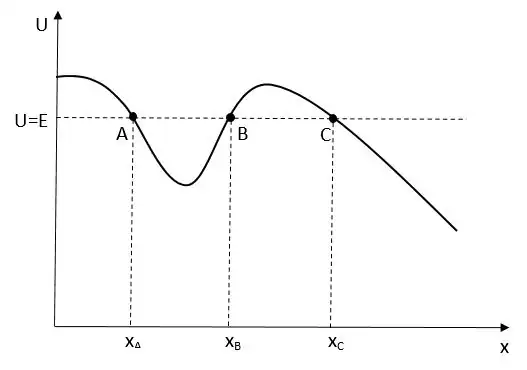
Движение системы с полной энергией E, может происходить только в области ${\displaystyle x_{_{A}}<x<x_{_{B}}}$ или в области ${\displaystyle x>x_{_{C}}}$, на графике. В точках, где кинетической энергии нет, а значит скорость равна нулю, потенциальная энергия равна полной ${\displaystyle U(x)=E}$, такие точки называются «границами движения» или «точками остановки».

Если область движения ограничена двумя точками остановки, то движение происходит в ограниченной области пространства. Такое движение называют «финитным».

Если область движения не ограничена или ограничена с одной стороны, то движение называется «инфинитным». При таком движении траектория частицы уходит в бесконечность.

Одномерное финитное движение является колебательным: частица совершает периодически повторяющееся движение между двумя границами. Область, в которой совершается такое движение (на рисунке это область ${\displaystyle x_{_{A}}<x<x_{_{B}}}$), называется «потенциальной ямой». Поскольку время изотропно, то время движения от ${\displaystyle x_{_{A}}}$ до ${\displaystyle x_{_{B}}}$, должно быть равно времени движения от ${\displaystyle x_{_{B}}}$ до ${\displaystyle x_{_{A}}}$. Поэтому, в общем случае, период колебаний можно найти как удвоенное время прохождения отрезка, равного «ширине» потенциальной ямы:

${\displaystyle \displaystyle T(E)={\sqrt {2m}}\int \limits _{x_{1}(E)}^{x_{2}(E)}{\frac {dx}{\sqrt {E-U(x)}}}}$ (1.4.7)

Формула   (1.4.7)   , определяет период финитного движения в зависимости от полной энергии. Пределы интегрирования ${\displaystyle x_{1}(E)}$;${\displaystyle x_{2}(E)}$ – это корни уравнения ${\displaystyle U(x)=E}$.

<<Назад  |  Далее>>
Оглавление