Основы теоретической физики/Свойства функции Лагранжа

1. Уравнения движения каждой из невзаимодействующих частей не могут содержать величины, относящиеся к другим частям системы.

Доказательство:

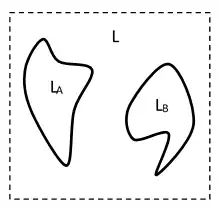
Чтобы исключить из рассмотрения взаимодействие между системами, достаточно развести эти системы на достаточно далекое расстояние друг от друга.

На рис.1.2 показаны две невзаимодействующих системы A и B, которым соответствуют функции Лагранжа LA и LB. Пусть эти системы являются частями одной замкнутой системы с функцией Лагранжа L. Поскольку уравнения движения  (1.1.24) 

являются линейными, получается, что при разведении частей настолько далеко, чтобы взаимодействием можно было пренебречь, функция Лагранжа всей системы действительно стремится к пределу:

${\displaystyle \lim L=L_{A}+L_{B}}$ (1.1.25)

Свойство   (1.1.25)    называется «свойством аддитивности» функции Лагранжа.

2. Функция Лагранжа определена с точностью до прибавления к ней полной производной от любой функции координат и времени.

Доказательство:
рассмотрим две функции и . Пусть эти функции отличаются друг от друга на полную производную по времени от какой-либо функции  :

${\displaystyle L^{\prime }(q,{\dot {q}},t)=L(q,{\dot {q}},t)+{\frac {d}{dt}}f(q,t)}$ (1.1.26)

тогда для действия будем иметь формулу:

${\displaystyle {\begin{array}{c}S^{\prime }=\displaystyle \int \limits _{t_{1}}^{t_{2}}L^{\prime }(q,{\dot {q}},t)dt=\displaystyle \int \limits _{t_{1}}^{t_{2}}L(q,{\dot {q}},t)dt+\displaystyle \int \limits _{t_{1}}^{t_{2}}{\frac {d}{dt}}f(q,t)\\S^{\prime }=S+f(q_{2},t_{2})-f(q_{1},t_{1})\end{array}}}$ (1.1.27)

Согласно принципу наименьшего действия, для вариаций имеем:

${\displaystyle \left.\displaystyle {\begin{array}{ccc}\delta S=0\\\delta S^{\prime }=0\\\end{array}}\right\}\Rightarrow \delta (f(q_{2},t_{2})-f(q_{1},t_{1}))=0}$ (1.1.28)

То есть действие отличается от действия на величину, которая исчезает (обнуляется) при варьировании. Значит второе слагаемое в   (1.1.26)    никак не влияет на решения уравнений движения   (1.1.24)   , что и требовалось доказать.

<<Назад  |  Далее>>
Оглавление