3-bit Walsh permutation/matrix columns/inverses

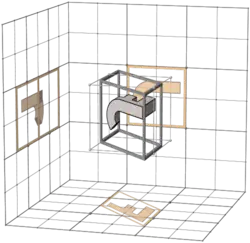
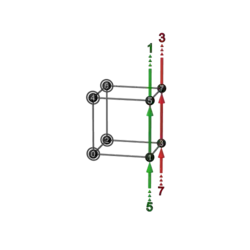
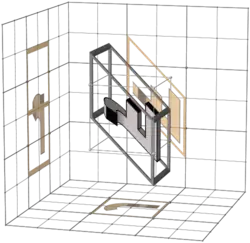
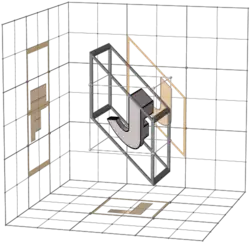
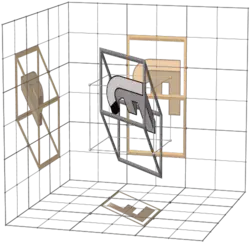
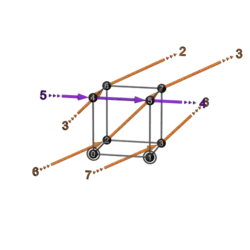
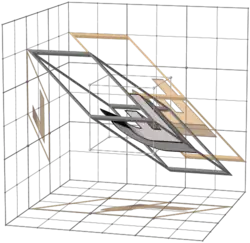
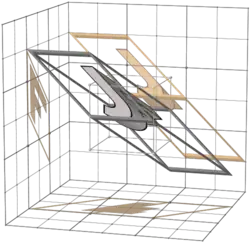
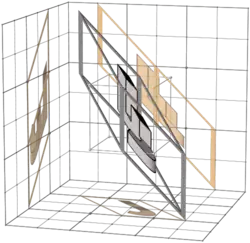
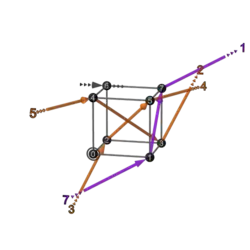
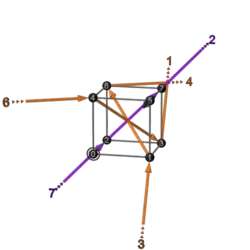
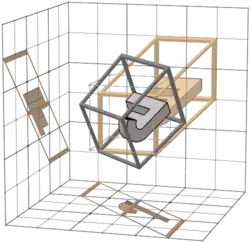
This is like the big table in 3-bit Walsh permutation/matrix columns, but (apart from the first row) the transforms are made not with binary matrices, but with inverses of binary matrices.
The non-zero entries are in the same places as in the corresponding binary matrix, but some entries are negative 1s.

cc	cs	cp	t	main	positive			negative
&0 neut.	&0 neut. 3	37	124	124	241	124	412	214	421	142
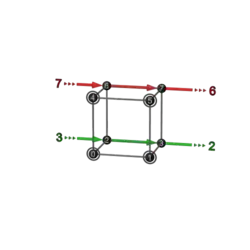2+2	&1 P 4	26	134	134	341	134	413	314	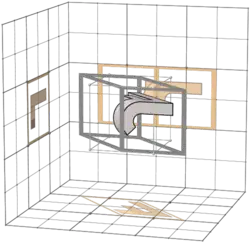431	143
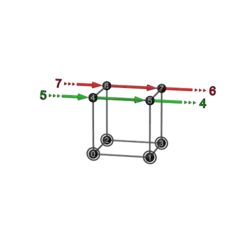2+2	&1 P 4	26	125	125	251	125	512	215	521	152
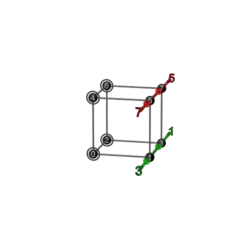2+2	&1 P 4	25	234	324	243	324	432	234	423	342
2+2	&1 P 4	25	126	126	261	126	612	216	621	162
2+2	&1 P 4	23	245	524	245	524	452	254	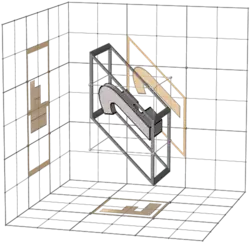425	542
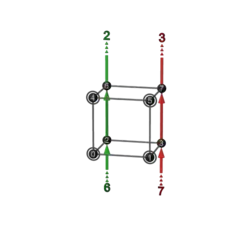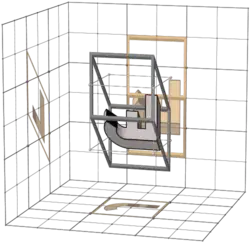2+2	&1 P 4	23	146	164	641	164	416	614	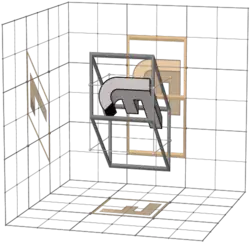461	146
2+2	&2 R 5a	11	247	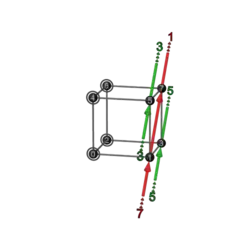724	247	724	472	274	427	742
2+2	&2 R 5a	12	147	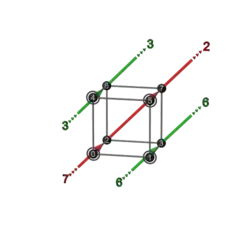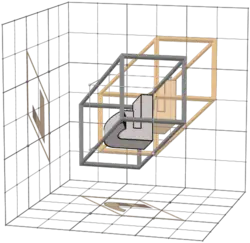174	741	174	417	714	471	147
2+2	&2 R 5a	14	127	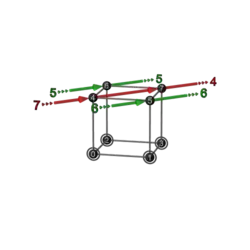127	271	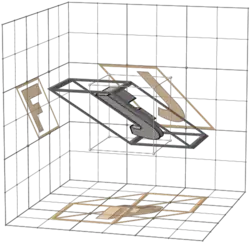127	712	217	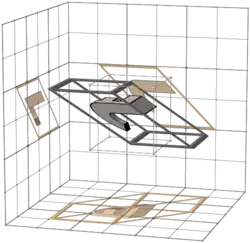721	172
2+2	&3 F 5a	37	13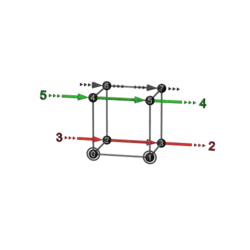5	135	351	135	513	315	531	153
2+2	&3 F 5a	37	23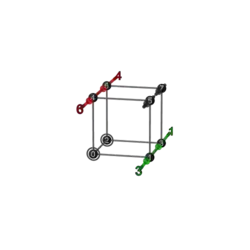6	326	263	326	632	236	623	362
2+2	&3 F 5a	37	45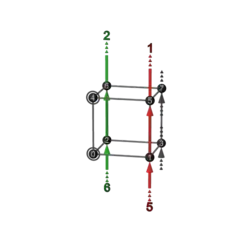6	564	645	564	456	654	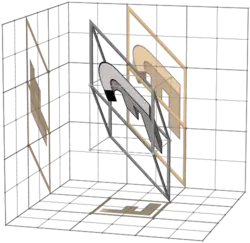465	546
2+4	&4 BA 5 5b	12	156	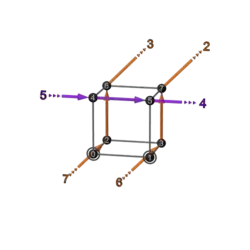165	651	165	516	615	561	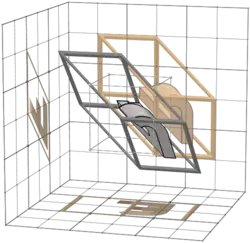156
2+4	&4 BA 5 5b	14	136	136	361	136	613	316	631	163
2+4	&4 BA 5 5b	14	235	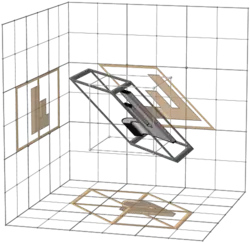325	253	325	532	235	523	352
2+4	&4 BA 5 5b	11	256	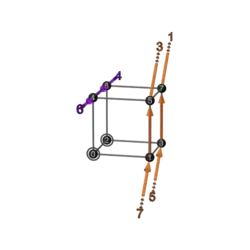526	265	526	652	256	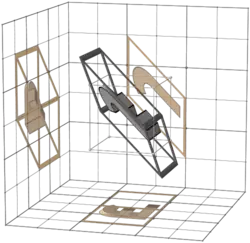625	562
2+4	&4 BA 5 5b	12	345	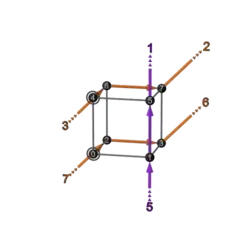534	345	534	453	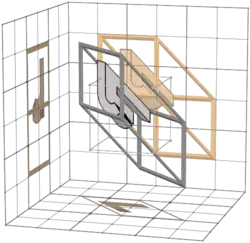354	435	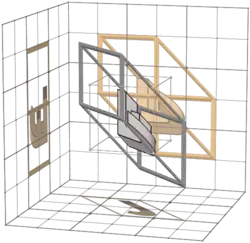543
2+4	&4 BA 5 5b	11	346	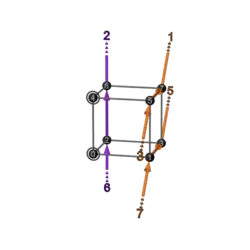364	643	364	436	634	463	346
2+4	&5 BA 6 6	23	157	175	751	175	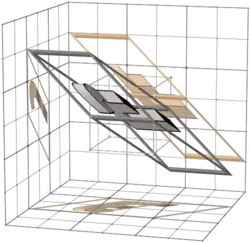517	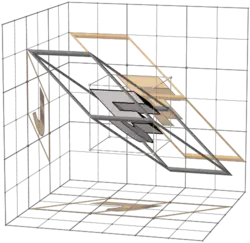715	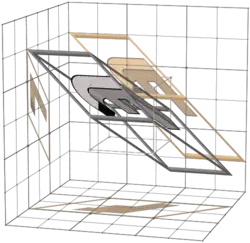571	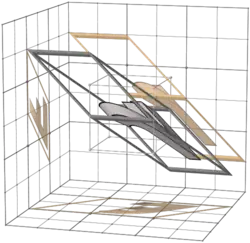157
2+4	&5 BA 6 6	25	137	137	371	137	713	317	731	173
2+4	&5 BA 6 6	23	267	726	267	726	672	276	627	762
2+4	&5 BA 6 6	26	237	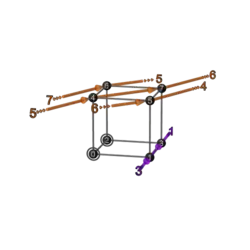327	273	327	732	237	723	372
2+4	&5 BA 6 6	25	467	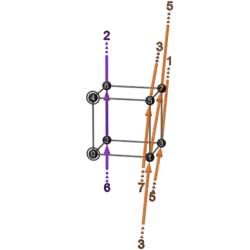764	647	764	476	674	467	746
2+4	&5 BA 6 6	26	457	574	745	574	457	754	475	547
7a	&6 S +7	11	357	753	537	753	375	573	357	735
7a	&6 S +7	12	367	673	736	673	367	763	376	637
7a	&6 S +7	14	567	657	576	657	765	567	756	675