Complex Analysis/Path of Integration

The following definitions were abbreviated with acronyms and are used as justifications for transformations or conclusions in proofs.

• (WG1) Definition (Smooth path): A path ${\displaystyle \gamma :[a,b]\to \mathbb {C} }$ is smooth if it is continuously differentiable.
• (UT) Definition (Subdivision): Let ${\displaystyle [a,b]}$ be an interval, ${\displaystyle n\in \mathbb {N} }$ and ${\displaystyle {a}={u}_{0}<{\ldots }<{u}_{n}={b}}$. ${\displaystyle {\left({u}_{0},\ldots ,{u}_{n}\right)}\in \mathbb {R} ^{n+1}}$ is called a subdivision of ${\displaystyle {\left[{a},{b}\right]}}$.
• (WG2) Definition (Path subdivision): Let ${\displaystyle \gamma :[a,b]\to \mathbb {C} }$ be a path in ${\displaystyle {U}\subseteq \mathbb {C} }$, ${\displaystyle {n}\in \mathbb {N} }$, ${\displaystyle {\left({u}_{0},\ldots ,{u}_{n}\right)}}$ a subdivision of ${\displaystyle [a,b]}$, ${\displaystyle \gamma _{k}:{\left[{u}_{{k}-{1}},{u}_{k}\right]}\to \mathbb {C} }$ for all ${\displaystyle {k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }}$ a path in ${\displaystyle {U}}$. ${\displaystyle {\left(\gamma _{1},\ldots ,\gamma _{n}\right)}}$ is called a path subdivision of ${\displaystyle \gamma }$ if ${\displaystyle \gamma _{n}{\left({b}\right)}=\gamma {\left({b}\right)}}$ and for all ${\displaystyle {k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }}$ and ${\displaystyle {t}\in {\left[{u}_{{k}-{1}},{u}_{k}\right]}}$ we have ${\displaystyle \gamma _{k}{\left({t}\right)}=\gamma {\left({t}\right)}\wedge \gamma _{k}{\left({u}_{{k}-{1}}\right)}=\gamma _{{k}-{1}}{\left({u}_{k}\right)}}$.
• (WG3) Definition (Piecewise smooth path): A path ${\displaystyle \gamma :{\left[{a},{b}\right]}\to \mathbb {C} }$ is piecewise smooth if there exists a path subdivision ${\displaystyle {\left(\gamma _{1},\ldots \gamma _{n}\right)}}$ of ${\displaystyle \gamma }$ consisting of smooth paths ${\displaystyle \gamma _{k}}$ for all ${\displaystyle {k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }}$.

• (WG4) Definition (Path integral): Let ${\displaystyle f:U\to \mathbb {C} }$ be a continuous function and ${\displaystyle \gamma :[a,b]\to U}$ a smooth path, then the path integral is defined as: ${\displaystyle \int _{\gamma }f:=\int _{\gamma }f(z)\,dz:=\int _{a}^{b}f(\gamma (t))\cdot \gamma '(t)\,dt}$. If ${\displaystyle \gamma }$ is only piecewise smooth with respect to a path subdivision ${\displaystyle (\gamma _{1},\ldots ,\gamma _{n})}$, then we define ${\displaystyle \int _{\gamma }f(z)\,dz:=\sum _{k=1}^{n}\int _{\gamma _{k}}f(z)\,dz}$.
• Definition (Integration path): An integration path is a piecewise smooth (piecewise continuously differentiable) path.

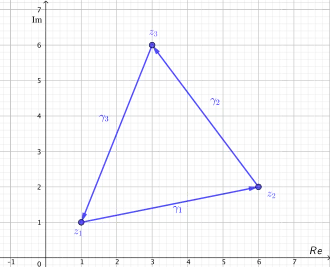
The following path is piecewise continuously differentiable (smooth) and for the vertices ${\displaystyle z_{1},z_{2},z_{3}\in {\text{Spur}}(\gamma )}$ the closed triangle path ${\displaystyle \gamma :[0,3]\to \mathbb {C} }$ is not differentiable. The triangle path is defined on the interval ${\displaystyle [0,3]}$ as follows:

${\displaystyle \gamma (t):=\left\langle z_{1},z_{2},z_{3}\right\rangle (t):={\begin{cases}(1-t)\cdot z_{1}+t\cdot z_{2}&{\text{for }}t\in [0,1]\\(2-t)\cdot z_{2}+(t-1)\cdot z_{3}&{\text{for }}t\in (1,2]\\(3-t)\cdot z_{3}+(t-2)\cdot z_{1}&{\text{for }}t\in (2,3]\\\end{cases}}}$

The piecewise continuously differentiable path is formed from convex combination.The sub-paths

• ${\displaystyle \gamma _{1}:=\left\langle z_{1},z_{2}\right\rangle }$ with ${\displaystyle \gamma _{1}:[0,1]\to \mathbb {C} ,\ (1-t)\cdot z_{1}+t\cdot z_{2}}$
• ${\displaystyle \gamma _{2}:=\left\langle z_{2},z_{3}\right\rangle }$ with ${\displaystyle \gamma _{2}:[1,2]\to \mathbb {C} ,\ (2-t)\cdot z_{2}+(t-1)\cdot z_{3}}$
• ${\displaystyle \gamma _{3}:=\left\langle z_{3},z_{1}\right\rangle }$ with ${\displaystyle \gamma _{3}:[2,3]\to \mathbb {C} ,\ (3-t)\cdot z_{3}+(t-2)\cdot z_{1}}$

are continuously differentiable.

• Goursat's Lemma (Details)
• convex combination
• Convex combinations and interpolation on triangles in the plane

This learning resource can be presented as a (Wiki2Reveal slides)

This (Wiki2Reveal slides) was created for the learning unit Complex Analysis'. The link for the Wiki2Reveal Slides was created with the link generator.

• of Integration This page] was created as a document type PanDocElectron-SLIDE .

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

• Source: Kurs:Funktionentheorie/Integrationsweg - URL: https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Integrationsweg
• Date: 11/20/2024