Definition: Path
Let
U
⊂
C
{\displaystyle U\subset \mathbb {C} }
U
{\displaystyle U}
continuous mapping with:
γ
:
[
a
,
b
]
→
U
{\displaystyle \gamma \colon [a,b]\rightarrow U}
a
<
b
{\displaystyle a<b}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
Definition: Trace of a Path
The trace of a path
γ
:
[
a
,
b
]
→
U
{\displaystyle \gamma \colon [a,b]\rightarrow U}
U
⊂
C
{\displaystyle U\subset \mathbb {C} }
image or range of the function
γ
{\displaystyle \gamma }
T
r
a
c
e
(
γ
)
:=
γ
(
t
)
∈
C
|
t
∈
[
a
,
b
]
{\displaystyle \mathrm {Trace} (\gamma ):={\gamma (t)\in \mathbb {C} \ |\ t\in [a,b]}}
Definition: Closed Path
Let
γ
:
[
a
,
b
]
→
U
{\displaystyle \gamma \colon [a,b]\rightarrow U}
U
⊂
C
{\displaystyle U\subset \mathbb {C} }
γ
{\displaystyle \gamma }
γ
(
a
)
=
γ
(
b
)
{\displaystyle \gamma (a)=\gamma (b)}
Definition: Region
Let
U
⊂
C
{\displaystyle U\subset \mathbb {C} }
C
{\displaystyle \mathbb {C} }
U
{\displaystyle U}
Definition: Path-Connected
Let
U
⊂
C
{\displaystyle U\subset \mathbb {C} }
U
{\displaystyle U}
:⟺
∀
z
1
,
z
2
∈
U
∃
γ
:
[
a
,
b
]
→
U
:
γ
(
a
)
=
z
1
∧
γ
(
b
)
=
z
2
∧
S
p
u
r
(
γ
)
⊆
U
{\displaystyle :\Longleftrightarrow \ \forall _{z_{1},z_{2}\in U}\exists _{\gamma \colon [a,b]\rightarrow U}:\ \gamma (a)=z_{1}\wedge \gamma (b)=z_{2}\wedge {Spur}(\gamma )\subseteq U}
Definition: Domain
Let
G
⊂
C
{\displaystyle G\subset \mathbb {C} }
C
{\displaystyle \mathbb {C} }
G
{\displaystyle G}
G
{\displaystyle G}
Then
G
{\displaystyle G}
C
{\displaystyle \mathbb {C} }
Example (Circular Paths)
Let
z
o
∈
C
{\displaystyle z_{o}\in \mathbb {C} }
r
>
0
{\displaystyle r>0}
γ
z
o
,
r
:
[
0
,
2
π
]
→
C
{\displaystyle \gamma _{z_{o},r}\colon [0,2\pi ]\rightarrow \mathbb {C} }
z
o
∈
C
{\displaystyle z_{o}\in \mathbb {C} }
γ
z
o
,
r
(
t
)
:=
z
o
+
r
⋅
e
i
⋅
t
{\displaystyle \gamma _{z_{o},r}(t):=z_{o}+r\cdot e^{i\cdot t}}
Example - Paths with Ellipse as Trace
Let
z
o
∈
C
{\displaystyle z_{o}\in \mathbb {C} }
a
,
b
>
0
{\displaystyle a,b>0}
γ
z
o
,
a
,
b
:
[
0
,
2
π
]
→
C
{\displaystyle \gamma _{z_{o},a,b}\colon [0,2\pi ]\rightarrow \mathbb {C} }
z
o
∈
C
{\displaystyle z_{o}\in \mathbb {C} }
γ
z
o
,
a
,
b
(
t
)
:=
z
o
+
a
⋅
cos
(
t
)
+
i
⋅
b
⋅
sin
(
t
)
{\displaystyle \gamma _{z_{o},a,b}(t):=z_{o}+a\cdot \cos(t)+i\cdot b\cdot \sin(t)}
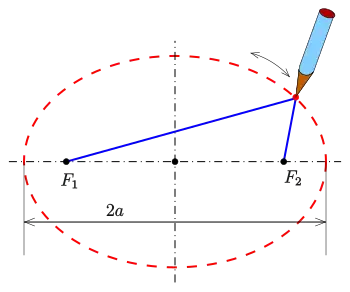
Gardener's Construction of an Ellipse
Convex Combinations
Let
z
1
,
z
2
∈
C
{\displaystyle z_{1},z_{2}\in \mathbb {C} }
t
∈
[
0
,
1
]
{\displaystyle t\in [0,1]}
γ
z
1
,
z
2
:
[
0
,
1
]
→
C
{\displaystyle \gamma _{z_{1},z_{2}}\colon [0,1]\rightarrow \mathbb {C} }
z
1
,
z
2
∈
C
{\displaystyle z_{1},z_{2}\in \mathbb {C} }
γ
z
1
,
z
2
(
t
)
:=
(
1
−
t
)
⋅
z
1
+
t
⋅
z
2
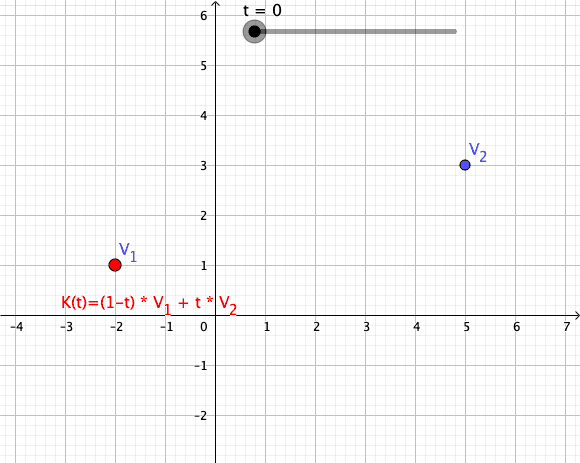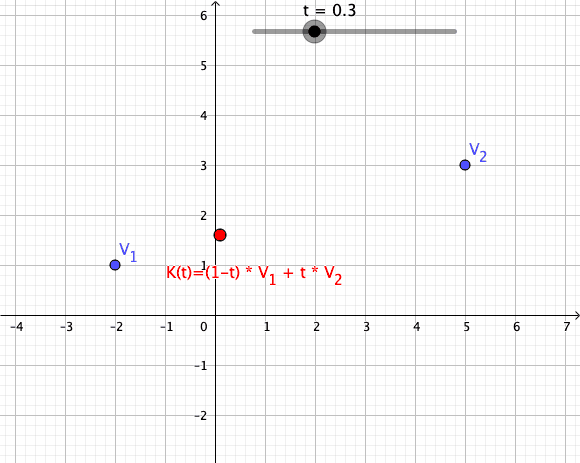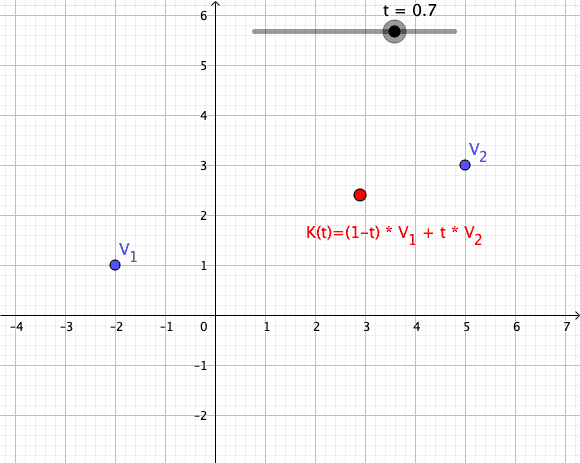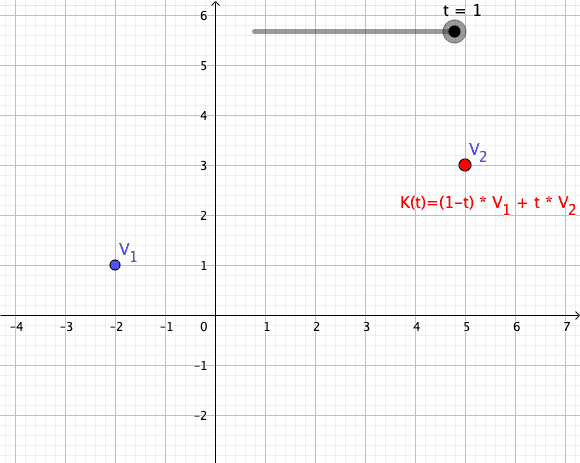
{\displaystyle \gamma _{z_{1},z2}(t):=(1-t)\cdot z_{1}+t\cdot z_{2}}
Such a path is called a convex combination of the first order (see also Convex Combinations of higher order ).
Animation of a Convex Combination of Two Vectors as Mapping
Convex Combination as Mapping in an Animated GIF
Integration Path
Let
G
⊂
C
{\displaystyle G\subset \mathbb {C} }
G
{\displaystyle G}
γ
:
[
a
,
b
]
→
U
{\displaystyle \gamma \colon [a,b]\rightarrow U}
a
<
b
{\displaystyle a<b}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
An integration path can, for example, be expressed piecewise as convex combinations between multiple points
z
1
,
…
z
n
∈
C
{\displaystyle z_{1},\ldots z_{n}\in \mathbb {C} }
z
1
,
…
z
n
∈
C
{\displaystyle z_{1},\ldots z_{n}\in \mathbb {C} }
See Also
Page Information
You can display this page as
Wiki2Reveal slides
Wiki2Reveal
TheWiki2Reveal slides Complex Analysis 'Wiki2Reveal Slides was created with the link generator .
Translation and Version Control
This page was translated based on the following [https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Wege
Wikiversity source page] and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:
https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Wege