Sample homework problems
Wedge loaded transversely by a concentrated load
Given:
A wedge of infinite length with a concentrated load  per
unit wedge thickness at the vertex. Plane stress/strain.
per
unit wedge thickness at the vertex. Plane stress/strain.
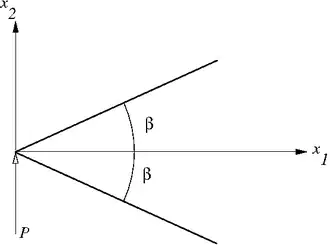 Wedge loaded transversely by a concentrated load Wedge loaded transversely by a concentrated load
|
Find:
The stress field in the wedge.
Solution
From the Flamant solution, we know that the stress field in the wedge is

The constants  and
and  can be found by using the equilibrium
conditions
can be found by using the equilibrium
conditions

or,
![{\displaystyle {\begin{aligned}C_{1}\left[2\beta +\sin(2\beta )\right]&=0\\P+C_{2}\left[\sin(2\beta )-2\beta \right]&=0\end{aligned}}}](../6a39e53f232f6f2f66c9044a485cc264b3c5ce4b.svg)
Therefore,

Hence, the stresses are
![{\displaystyle {\begin{aligned}\sigma _{rr}&={\frac {2P\sin \theta }{r\left[2\beta -\sin(2\beta )\right]}}\\\sigma _{r\theta }&=0\\\sigma _{\theta \theta }&=0\end{aligned}}}](../b2733d8e3fdd09c065548909a28b97b1732a41d2.svg)
