Topological space
A topological space is the fundamental subject of the subdiscipline topology of mathematics. By introducing a topological structure on a set, it is possible to establish.
- intuitive positional relations like "proximity" and
- "convergence against" from the real numbers
 or from the
or from the  , respectively.
, respectively.
to many and very general structures (such as the topology of function spaces).
Definition: topology
A topology is a set system  consisting of subsets (open sets) of a basic set
consisting of subsets (open sets) of a basic set  for which the following axioms are satisfied.
for which the following axioms are satisfied.
- (T1)

- (T2)
 for all
for all  .
.
- (T3) For any index set
 and
and  for all
for all  holds:
holds:  .
.
A set  together with a topology
together with a topology  on
on  is called topological space
is called topological space  .
.
By defining all open sets in  by the topology
by the topology  , all closed sets are also defined as complements of an open set
, all closed sets are also defined as complements of an open set  .
.

Definition - open kernel of a set
Let  be in the topological space
be in the topological space  , then the open core
, then the open core  is defined as the "largest" open set contained in
is defined as the "largest" open set contained in  :
:

Since in the definition  is represented as the union of open sets
is represented as the union of open sets  ,
,  open by axiom (T3).
open by axiom (T3).
Definition - connection of a set
Let  be in the topological space
be in the topological space  , then the closure
, then the closure  is defined as the "smallest" closed set containing
is defined as the "smallest" closed set containing  :
:

Since in the definition  is represented as the intersection of closed sets
is represented as the intersection of closed sets  with
with  ,
,  is again open as the completion of any union of open sets, since it holds again according to (T3):
is again open as the completion of any union of open sets, since it holds again according to (T3):

Definition - Boundary of a set
Let  be a set in the topological space
be a set in the topological space  , then the edge of a set from the closure of the set
, then the edge of a set from the closure of the set  without the open core
without the open core  of
of  . The boundary is therefore defined as follows:
. The boundary is therefore defined as follows:
 .
.
The sets  are by definition open and mutually the two sets form the complements of each other. Thus these two sets are both open and closed at the same time. Therefore, the two sets have no boundary points.
are by definition open and mutually the two sets form the complements of each other. Thus these two sets are both open and closed at the same time. Therefore, the two sets have no boundary points.
Definition - Neighbourhood
Let  and
and  be a set in a topological space
be a set in a topological space  , then the
, then the  is called Neighbourhood of
is called Neighbourhood of  if there exists an open set
if there exists an open set  with:
with:

The set of all Neighbourhood of  with respect to the topology
with respect to the topology  is denoted by
is denoted by  .
.  denotes the set of all open neighbourhoods of
denotes the set of all open neighbourhoods of  .
.
Definition - Neighbourhood basis
Let  and
and  a set system in a topological space
a set system in a topological space  , then the \mathcal{B} is called the neighbourhood basis of
, then the \mathcal{B} is called the neighbourhood basis of  if the following properties hold:
if the following properties hold:
- (B1)

- (B2) for each environment
 a neighborhood
a neighborhood  with
with  .
.
Example
The set of open  neighbourhood
neighbourhood  in
in  with the Euclidean topology
with the Euclidean topology  generated by the amount
generated by the amount  is an neighbourhood basis of
is an neighbourhood basis of  .
.
The neighbourhood basis term helps to prove convergence statements for the neighbourhood basis only, and thus to obtain the statements for arbitrary neighbourhoods as well. In calculus one uses  -neighbourhoods in definitions without explicitly addressing the topological aspect of the neighbourhood basis, that proofs in general arbitrary neighbourhoods and not only for the neighbourhood basis. Due to the fact that an arbitrary neighbourhood contains a set of the neighbourhood basis, the most of the convergence proofs can limit themselves to the neighbourhood basis.
-neighbourhoods in definitions without explicitly addressing the topological aspect of the neighbourhood basis, that proofs in general arbitrary neighbourhoods and not only for the neighbourhood basis. Due to the fact that an arbitrary neighbourhood contains a set of the neighbourhood basis, the most of the convergence proofs can limit themselves to the neighbourhood basis.
Definition - base of topology
Let  and
and  be a set system in a topological space
be a set system in a topological space  , then the
, then the  is called the basis of
is called the basis of  if holds:
if holds:
- (BT1)

- (BT2) for every open set
 there is an open set
there is an open set  with
with  .
.
Example
The set of all open intervals  is a basis of the topology in the topological
is a basis of the topology in the topological  with the Euclidean topology
with the Euclidean topology  generated by the amount
generated by the amount  .
.
Convergence in topological spaces
In calculus, the convergence of sequences is a central definition to define notions based on it, such as continuity, difference, and integrals. Sequences  with
with  as index set are unsuitable to define convergence in general topological spaces, because the index set
as index set are unsuitable to define convergence in general topological spaces, because the index set  is not powerful enough concerning the neighbourhood basis. This is only possible if the topological space has a countable neighbourhood basis. Therefore one goes over either to nets or Filters
is not powerful enough concerning the neighbourhood basis. This is only possible if the topological space has a countable neighbourhood basis. Therefore one goes over either to nets or Filters
Example: topology on texts
Usually, one assumes that topologies are defined on mathematical spaces (e.g., number spaces, function spaces, (topological) groups, vector spaces, ...). However, the generality of the definition makes it also possible to define a topology on texts. This example was added because purely descriptively, e.g., texts in the German language
- can have a similar statement and
- use different words.
This similarity of semantics, or syntax, is explored in more detail as an exercise in "Topology on Texts".
Describe similarity of words by metrics
From spoken words, represent the number of letters and the set of occurring letters as a table. How can you derive a distance of words from the tabulated list. make a suggestion for this. What are the properties of your proposed distance function. Is it a metric on the space of words?
Task - distance between words
- Consider the words "bucket", "buket", "buckett". How can you express the differences of the words by a metric
- Phonetic similarity words "bucket" and "pucket" have a phonetic similarity, but from the sequence of letters the spellings differ greatly. How can you notate similarity of spoken words (Speech Recognition) by a phonetic notation and in this notation of phonemes express a similarity of words as well.
Classification of topological spaces
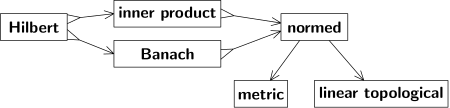
Meaning of Properties topology
- (T1)
 empty set and the basic set
empty set and the basic set  are open sets.
are open sets.
- (T2)
 for all
for all  : the average of finitely many open sets is an open set.
: the average of finitely many open sets is an open set.
- (T3) The union of any many open sets is again an open set.
Semantics: metric
A metric  associates with
associates with  two elements
two elements  from a base space
from a base space  the distance
the distance  between
between  and
and  .
.
Definition: Metric
Let  be an arbitrary set. A mapping
be an arbitrary set. A mapping  is called a metric on
is called a metric on  if for any elements
if for any elements  ,
,  and
and  of
of  the following axioms are satisfied:
the following axioms are satisfied:
- (M1) separation:
 ,
,
- (M2) symmetry:
 ,
,
- (M3) triangle inequality:
 .
.
Illustration: metric triangle inequality
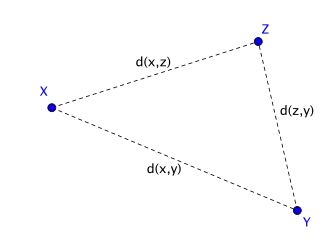
According to the triangle inequality, the distance between two points X,Y is at most as large as sum of the distances from X to Z and from Z to Y, that is, a detour via the point Z
Non-negativity
Non-negativity follows from the three properties of the metric, i.e. for all  holds.
holds.  . The non-negativity follows from the other properties with:
. The non-negativity follows from the other properties with:
 .
.

Open sets in metric spaces
- In a metric space
 , one defines a set
, one defines a set  to be open (i.e.
to be open (i.e.  ) if for every
) if for every  there is a
there is a  that the
that the  -sphere
-sphere  lies entirely in
lies entirely in  (i.e. i.e.
(i.e. i.e.  )
)
- Show that with this defined
 , the pair
, the pair  is a topological space (i.e., (T1), (T2), (T3) satisfied).
is a topological space (i.e., (T1), (T2), (T3) satisfied).
Norm on vector spaces
A norm is a mapping  from a vector space
from a vector space  over the body
over the body  of the real or the complex numbers into the set of nonnegative real numbers
of the real or the complex numbers into the set of nonnegative real numbers  . Here the norm assigns to each vector
. Here the norm assigns to each vector  its length
its length  .
.
Definition: Norm
Let  be a
be a  vector space and
vector space and  a mapping.
If
a mapping.
If  satisfies the following axioms axioms N1,N2, N3, then
satisfies the following axioms axioms N1,N2, N3, then  is called a norm on
is called a norm on  .
.
- (N1) Definiteness:
 for all
for all  ,
,
- (N2) absolute homogeneity:
 for all
for all  and
and  .
.
- (N3) Triangle inequality:
 for all
for all  .
.
The property (N1) is actually an equivalence and it holds in any normed space. If  is the zero vector in
is the zero vector in  and
and  is the zero in the field
is the zero in the field  , if
, if  is a
is a  vector space).
vector space).
- (N1)' definiteness:
 for all
for all  ,
,
- Since one uses a minimality principle for definitions for the defining property, one would not use a stronger formulation (N1)' in the definition for (N1), since the equivalence from the defining properties of the norm follow the properties of the vector space already for any normed space.

Normed space / Metric space
A normed space  is also a metric space.
is also a metric space.
- A norm
 assigns to a vector
assigns to a vector  its vector length
its vector length  .
.
- The norm
 can be used to define a metric via
can be used to define a metric via  that specifies the distance between
that specifies the distance between  and
and  .
.
Learning Task: generate metric from given norm
Let  be a normed space with norm
be a normed space with norm  .
Show that the defined mapping
.
Show that the defined mapping  with
with  satisfies the properties of a metric.
satisfies the properties of a metric.
Notation: norm
- In the axiom (N2)
 ,
,  denotes the amount of the scalar. "
denotes the amount of the scalar. " " sign: Outer linkage in vector space or multiplication
" sign: Outer linkage in vector space or multiplication  .
.
 indicates the length of the vector
indicates the length of the vector  .
.- In (N3)
 for all
for all  . '"
. '" "-sign denotes two distinct links (i.e., addition in
"-sign denotes two distinct links (i.e., addition in  and
and  , respectively.
, respectively.
Illustration: norm triangle inequality
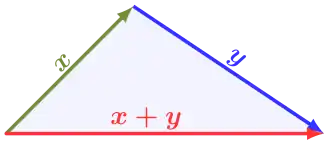 mini
mini
Def: convergence in normalized space
Let  be a normalized space and
be a normalized space and  a sequence in
a sequence in  and
and  :
:

Def: convergence in metric space
Let  be a metric space and
be a metric space and  a sequence in
a sequence in  and
and  :
:

Def: Cauchy sequences in metric spaces
Let  be a metric space and
be a metric space and  a sequence in
a sequence in  .
.  is called a Cauchy sequence in
is called a Cauchy sequence in  :
:

Equivalence: norms
Let two norms  and
and  be given on the
be given on the  vector space
vector space  . The two norms are equivalent if holds:
. The two norms are equivalent if holds:
 .
.
Show that a sequence converges in  exactly if it also converges with respect to
exactly if it also converges with respect to  .
.
Absolute value in complex numbers
Let  be a complex number with
be a complex number with  . Show that
. Show that  is a norm on the
is a norm on the  vector space
vector space  !
!
Historical Notes: Norm
This axiomatic definition of norm was established by Stefan Banach in his 1922 dissertation. The norm symbol in use today was first used by Erhard Schmidt in 1908 as the distance  between vectors
between vectors  and
and  .
.
See also
Page Information
You can display this page as Wiki2Reveal slides
Wiki2Reveal
The Wiki2Reveal slides were created for the Functional analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.


 mini
mini