Report 6
Problem 1
Problem Statement
ODE: 
Part 1: show that cos7x and sin7x are linearly independent using the Wronskian and Gramian.
Part 2: Find 2 equations for the two unknowns M, N, and solve for M, N.
Part 3: Find the overall solution y(x) that corresponds to the initial conditions: 
Plot the solution over 3 periods
Solution
Part 1
Wronskian: Function is linearly independent if 




g(x) and f(x) are linearly independent
Gramian: Function is linearly independent if 







g(x) and f(x) are linearly independent
Part 2
The particular solution for a  will be:
will be:

Differentiate to get:


Plug the derivatives into the equation:


Separate the sin and cos terms to get 2 equations in order to solve for M and N


dividing each equation by cos7x and sin7x respectively:




So the particular solution is:

Part 3
The overall solution can be found by:

The roots given in the problem statement 
Lead to the homogeneous solution of:

Combining the homogeneous and particular solution gives us:

Solving for the constants by using the initial conditions 




The overall solution is:

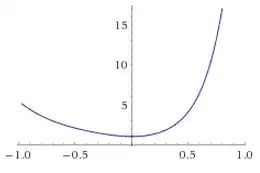
Plot
Plot 
over 3 periods:
Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 2
Problem Statement
Complete the solution to problem on p.8-6.
Find the overall solution 
that corresponds to the initial condition 
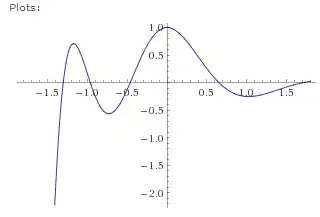
Plot solution over 3 periods.
Solution
Given:








Solve for M and N:



Using initial conditions given find A and B
After applying initial conditions, we get



Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 3
Problem Statement
Is the given function even or odd or neither even nor odd? Find its Fourier Series.
Solution

 so
so  is an even function.
is an even function.
The Fourier series is ![{\displaystyle f(x)=a_{0}+\sum _{n=1}^{\infty }[a_{n}cos(nwx)+b_{n}sin(nwx)]}](../../../572aa93560e3630683588a21c7ec56e16ddf8c5b.svg) .
.

For 


For 


The above integral requires two iterations of integration by parts. Which gives
![{\displaystyle a_{n}={\frac {1}{n\pi }}[sin(n\pi )-sin(-n\pi )]+{\frac {2}{n^{2}\pi ^{2}}}[cos(n\pi )+cos(-n\pi )]-{\frac {2}{n^{3}\pi ^{3}}}[sin(n\pi )-sin(-n\pi )]}](../../../d258d6131ac7db6db3bb6f452fefd88e4665da2a.svg)
Similarly, integration by parts needs to be used twice to solve the following integral.

![{\displaystyle b_{n}={\frac {-1}{n\pi }}[cos(n\pi )-cos(-n\pi )]+{\frac {2}{n^{2}\pi ^{2}}}[sin(n\pi )+sin(-n\pi )]+{\frac {2}{n^{3}\pi ^{3}}}[cos(n\pi )-cos(-n\pi )]}](../../../d1701f6016a8083df714cbc0dd71c9713fd9bcc6.svg)
So the Fourier series for  is
is
![{\displaystyle {\frac {1}{3}}+\sum _{n=1}^{\infty }cos(nwx)[{\frac {1}{n\pi }}[sin(n\pi )-sin(-n\pi )]+{\frac {2}{n^{2}\pi ^{2}}}[cos(n\pi )+cos(-n\pi )]-{\frac {2}{n^{3}\pi ^{3}}}[sin(n\pi )-sin(-n\pi )]]}](../../../4d1b3c785ae7c556a2ef2c7898b84e5b699ca899.svg)
![{\displaystyle +sin(nwx)[-{\frac {1}{n\pi }}[cos(n\pi )-cos(-n\pi )]+{\frac {2}{n^{2}\pi ^{2}}}[sin(n\pi )+sin(-n\pi )]+{\frac {2}{n^{3}\pi ^{3}}}[cos(n\pi )-cos(-n\pi )]]}](../../../1d9a819ff8a5c1b538d2e0c1f188752c8061c7d1.svg)
Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 4
Problem Statement
1) Develop the Fourier series of . Plot
. Plot and develop the truncated Fourier series
and develop the truncated Fourier series .
.
![{\displaystyle f_{n}({\bar {x}}):={\bar {a}}_{0}+\sum _{k=1}^{n}[{\bar {a}}_{k}\cos k\omega {\bar {x}}+{\bar {b}}_{k}\sin k\omega {\bar {x}}]}](../../../b4148a2e3b7a30083ad8bd117fa313bd2b8f2204.svg)
for n = 0,1,2,4,8. Observe the values of at the points of discontinuities, and the Gibbs phenomenon. Transform the variable so to obtain the
Fourier series expansion of . Level 1: n=0,1.
2)Do the same as above, but using to obtain the Fourier series expansion of
to obtain the Fourier series expansion of ; compare to the result obtained above. Level 1: n=0,1.
; compare to the result obtained above. Level 1: n=0,1.
Solution
Part 1
To begin, the function  was determined to be even. Even functions reduce to a cosine Fourier series.
Because
was determined to be even. Even functions reduce to a cosine Fourier series.
Because  , has a period of 4, the length is 2.
, has a period of 4, the length is 2.



![{\displaystyle f_{k}({\bar {x}})=a_{0}+\sum _{k=1}^{n}[a_{n}\cos {\frac {n\pi {\bar {x}}}{2}}]}](../../../6cc46d3cbd89239f72ac5880a5d2d543eb352c72.svg)
![{\displaystyle f_{k}={\frac {A}{2}}+\sum _{k=1}^{n}[{{\frac {2A}{k\pi }}\sin({\frac {k\pi }{2}})}\cos {\frac {k\pi {\bar {x}}}{2}}]}](../../../1e8c93229a59b63538e7e80387133e57164cd1b3.svg)
For n=0,

For n=1,



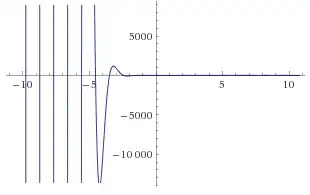
Plot (A=1)
.JPG)
Part 2
To begin, the function  was determined to be odd. Even functions reduce to a sine Fourier series.
Because
was determined to be odd. Even functions reduce to a sine Fourier series.
Because  , has a period of 4, the length is 2.
, has a period of 4, the length is 2.



 from 0 to 4
from 0 to 4


 from 0 to 4
from 0 to 4

![{\displaystyle f_{k}({\tilde {x}})={\frac {A}{2}}+\sum _{k=1}^{n}[{\frac {A}{k\pi }}(1-\cos(\pi k))(\sin({\frac {k\pi {\tilde {x}}}{2}}))]}](../../../933cdaee1e78aa31c54808efafc3dc19c3b120dc.svg)
For n=0,

For n=1,



Plot (A=1)
.JPG)
Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 5
Problem Statement
Find the separated ODE's for the Heat Equation:
 (1)
(1)
 heat capacity
heat capacity
Solution
Separation of Variables:
Assume: 
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
Plug (2) and (3) into Heat Equation (1):
 (6)
(6)
Rearrange (6) to combine like terms:







Solution:
Separated ODE's for Heat Equation:


Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 6
Problem Statement
Verify (4)-(5) p.19-9
(4) for
for 
(5) for
for 
Solution
Verification of (4)
Using the integral scalar product calculation,

Substituting in sin values,

Using  and
and 
You can substitute z into the integral instead of x.

Integrating,
![{\displaystyle {\frac {1}{2}}[{\frac {sin(i-j)z}{i-j}}-{\frac {sin(i+j)z}{i+j}}]}](../../../2ce36a3c8f876d2f7be13eb64e2a9a2867294867.svg) from
from  to
to 
Since  , the equation with its sin values turns into 0-0=0
, the equation with its sin values turns into 0-0=0
Verification of (5)
You can use the same equation from the verification of (4) from this point:
![{\displaystyle {\frac {1}{2}}[{\frac {sin(i-j)z}{i-j}}-{\frac {sin(i+j)z}{i+j}}]}](../../../2ce36a3c8f876d2f7be13eb64e2a9a2867294867.svg) from
from  to
to 
Putting those values in and substituting L back in the equation, it turns into 
Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.
Problem 7
Problem Statement

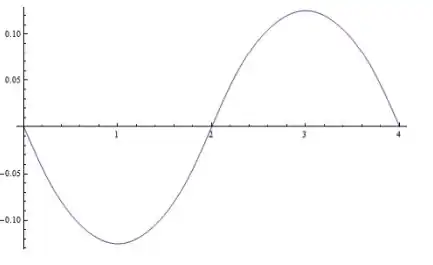
Plot the truncated series for n=5.


Solution
![{\displaystyle a_{j}={\frac {2[((-1)^{j})-1]}{\pi ^{3}j^{3}}}}](../../../e26da390654d425ff6ffa2e7c79e2834e53977a0.svg)

C=3 and L=2
Plot 

Plot 

Plot 

Plot 
Honor Pledge
On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.