Report 5
Intermediate Engineering Analysis
Section 7566
Team 11
Due date: March 30, 2012.
R5.1
Problem Statement
Given: Find  for the following series:
for the following series:
1. 
2. 
Find  for the Taylor series of
for the Taylor series of
3.  at
at 
4.  at
at 
5.  at
at 
Solution
The radius of convergence  is defined as
is defined as
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {d_{k+1}}{d_{k}}}|]^{-1}\!}](../../d6b8ccc715a7471923f69e28178706700849ca1f.svg)
1.
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(k+2)(k+1)}{(k+1)(k)}}|]^{-1}\!}](../../fc71081c7afee94390e37f71f56d2193dec48de9.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(k+2)}{(k)}}|]^{-1}\!}](../../b1af688ca1f47d693121b1271218fd929490e415.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {k(1+{\frac {2}{k}})}{k}}|]^{-1}\!}](../../91507d0db845548c113c47343de793dc125cf834.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|1+{\frac {2}{k}}|]^{-1}\!}](../../5c8a3989bc7fc0b444be04b556b2d2ee1c1a1d7d.svg)
![{\displaystyle R_{c}=[1+0]^{-1}\!}](../../ea6fe870b92b59fdd2dd61e493f66c583d007ff5.svg)

2.
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)^{k+1}}{\gamma ^{k+1}}}{\frac {(-1)^{k}}{\gamma ^{k}}}}|]^{-1}\!}](../../05386557debdb49583acce7ab9f83a1d4be70b88.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {-1}{\gamma }}|]^{-1}\!}](../../f4544068f0608761e16857dd77cca7662123056f.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }{\frac {1}{\gamma }}]^{-1}\!}](../../7997241d23909c23c91497322fbe1ff149d57d78.svg)
![{\displaystyle R_{c}=[{\frac {1}{\gamma }}]^{-1}\!}](../../1414ef0ffee2c582ed3eeaf9a7993a628b08b4d0.svg)

However, in this problem, the series  term is
term is  not
not  , as is the general form.
, as is the general form.
Therefore, this implies:



3. The Taylor series for  is expressed as
is expressed as 




Therefore:
![{\displaystyle R_{c}=[\lim _{k\to \infty }{\frac {1}{(2k+3)}}]^{-1}\!}](../../3b3f749928e2e6110c615a89db49b3e83b1ca1c5.svg)

4. The Taylor series for  at
at  is expressed as
is expressed as 
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)^{k+2}}{k+1}}{\frac {(-1)^{k+1}}{k}}}|]^{-1}\!}](../../1c89f760e5fa1462fac57cfd53e47c7ba4695f4d.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)}{k+1}}{\frac {(1)}{k}}}|]^{-1}\!}](../../e0fd04d810dc90cb7de776420e8b664f3ff32f6f.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)}{k(1+{\frac {1}{k}})}}{\frac {1}{k}}}|]^{-1}\!}](../../27d01121f5bf24b5b3c0f00bdc9fe4cea9fabdaf.svg)
![{\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(-1)}{(1+{\frac {1}{k}})}}|]^{-1}\!}](../../de135421582f0cd5c0506882a31fb79c9d191882.svg)
![{\displaystyle R_{c}=[1/1]^{-1}\!}](../../18d3becf975c7c5cb357e14fbb8da3130baba3f1.svg)

5. The Taylor series for  at
at  is expressed as
is expressed as 





For convergence: 


Therefore,

R5.2
Solved by: Andrea Vargas
Problem Statement
Part 1:Determine whether the following are linearly independent using the Wronskian
Part 2: Determine whether the following are linearly independent using the Gramian
Solution
Part 1
Using the Wronskian we check for linear independence.
We know from (1) and (2) in 7-35 that if

Then the functions are linearly independent.
Part 1.1


Taking the derivatives of each function:



 f(x) and g(x) are linearly independent
f(x) and g(x) are linearly independent
Part 1.2


Taking the derivatives of each function:



 f(x) and g(x) are linearly independent
f(x) and g(x) are linearly independent
Part 2
Using the Gramian we check for linear independence.
We know from the notes in (1) 7-34 that:

and that the Gramian is defined as:

Then f,g are linearly independent if 
Part 2.1


Taking scalar products:
![{\displaystyle \langle f,f\rangle :=\int _{-1}^{1}=f(x)f(x)=x^{2}*x^{2}=\int _{-1}^{1}=x^{4}=\left[{\frac {x^{5}}{5}}\right]_{-1}^{1}={\frac {2}{5}}\!}](../../c9558e9969a77a0045d0716d1f5ae91e7ddad89e.svg)
![{\displaystyle \langle f,g\rangle =\langle g,f\rangle :=\int _{-1}^{1}=f(x)g(x)=x^{2}*x^{4}=\int _{-1}^{1}=x^{6}=\left[{\frac {x^{7}}{7}}\right]_{-1}^{1}={\frac {2}{7}}\!}](../../602b892d340a3d3b15cdad195048562b0b4c3d81.svg)
![{\displaystyle \langle g,g\rangle :=\int _{-1}^{1}=g(x)g(x)=x^{4}*x^{4}=\int _{-1}^{1}=x^{8}=\left[{\frac {x^{9}}{9}}\right]_{-1}^{1}={\frac {2}{9}}\!}](../../c7ea937455865cedfe397a7909635c90e2c5c920.svg)

 f(x) and g(x) are linearly independent
f(x) and g(x) are linearly independent
Part 2.2


Taking scalar products:

We can use the trig identity for power reduction 
Then we have,
![{\displaystyle \int _{-1}^{1}{\frac {1}{2}}\cos(2x)+{\frac {1}{2}}dx=\left[{\frac {1}{4}}\sin(2x)+{\frac {1}{2}}x\right]_{-1}^{1}\!}](../../1b430bf3d0b57d4d80031e1c87c89e7e84cf1a67.svg)


![{\displaystyle =\int _{-1}^{1}\sin(3x)\cos(x)dx=\left[{\frac {1}{8}}(-2\cos(2x)-\cos(4x))\right]_{-1}^{1}\!}](../../8203ee3878256536c05c42f6634ab0d963539e6e.svg)


![{\displaystyle ={\frac {1}{2}}\int _{-1}^{1}1-\cos(6x)dx=\left[{\frac {1}{2}}(x-{\frac {1}{6}}\sin(6x))\right]_{-1}^{1}\!}](../../2ce4d0a3d02f4039abbee99ac372ff1fb6572374.svg)


 f(x) and g(x) are linearly independent
f(x) and g(x) are linearly independent
Conclusion
By both methods (the Wronskian and the Gramian) we obtain the same results.
R5.3
Problem Statement
Verify using the Gramian that the following two vectors are linearly independent.


Solution

We know from (3) 8-9 that:

We obtain,



Then,

 b_1 and b_2 are linearly independent
b_1 and b_2 are linearly independent
R5.4
Problem Statement
Show that  is indeed the overall particular solution of the L2-ODE-VC
is indeed the overall particular solution of the L2-ODE-VC  with the excitation
with the excitation  .
.
Discuss the choice of  in the above table e.g., for
in the above table e.g., for  why would you need to have both
why would you need to have both  and
and  in
in  ?
?
Solution
Because the ODE is a linear equation in y and its derivatives with respect to x, the superposition principle can be applied:
 is a specific excitation with known form of
is a specific excitation with known form of  and
and  is a specific excitation with known form of
is a specific excitation with known form of 

becomes

proving that
 is indeed the overall particular solution of the L2-ODE-VC
is indeed the overall particular solution of the L2-ODE-VC  with the excitation
with the excitation 
According to Fourier Theorem periodic functions can be represented as infinite series in terms of cosines and sines:
![{\displaystyle f(x)=a_{0}+\sum _{n=1}^{\infty }[a_{n}\cos \omega x+b_{n}\sin \omega x]\!}](../../1abd51ec088c597412c9e0bbb11e2628601e639e.svg)
where the coefficients  are the Fourier coefficients calculated using Euler formulas.
are the Fourier coefficients calculated using Euler formulas.
So even though the system is being excited by functions like  the particular solution would still include both
the particular solution would still include both  and
and  in
in  because the excitation is a periodic function that can be represented as the Fourier infinite series in terms of both
because the excitation is a periodic function that can be represented as the Fourier infinite series in terms of both  and
and  times the Fourier coefficients
times the Fourier coefficients
R5.5
Part 1
Problem Statement
Show that  and
and  are linearly independant using the Wronskian and the Gramain (integrate over 1 period)
are linearly independant using the Wronskian and the Gramain (integrate over 1 period)
Solution

One period of 
Wronskian of f and g

Plugging in values for 


![{\displaystyle =7[cos^{2}(7x)+sin^{2}(7x)]}](../../b301de567d6ca791f8580ee8e9e260a31d103757.svg)
![{\displaystyle =7[1]}](../../b92b8a5eea92d540f3a060ab9d154589aa005e48.svg)
They are linearly Independant using the Wronskian.







They are linearly Independent using the Gramain.
Problem Statement
Find 2 equations for the 2 unknowns M,N and solve for M,N.
Solution



Plugging these values into the equation given ( ) yields;
) yields;

Simplifying and the equating the coefficients relating sin and cos results in;


Solving for M and N results in;

Problem Statement
Find the overall solution  that corresponds to the initial conditions
that corresponds to the initial conditions  . Plot over three periods.
. Plot over three periods.
Solution
From before, one period  so therefore, three periods is
so therefore, three periods is 
Using the roots given in the notes  , the homogenous solution becomes;
, the homogenous solution becomes;

Using initial condtion  ;
;


with 

Solving for the constants;


Using the  found in the last part;
found in the last part;



R5.6
solved by Luca Imponenti
Problem Statement
Complete the solution to the following problem

where
![{\displaystyle y_{h}=e^{-2x}[Acos(3x)+Bsin(3x)]\!}](../../792e67f127ff688d55ed48d9f0303345b9a28184.svg)
and
![{\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}](../../96a697d5683642f371e1127b4a15314d1a2b93f0.svg)
Find the overall solution  corresponds to the initial condition:
corresponds to the initial condition:

Plot the solution over 3 periods.
Particular Solution
Taking the derivatives of the particular solution 
![{\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}](../../96a697d5683642f371e1127b4a15314d1a2b93f0.svg)
![{\displaystyle y'_{p}=e^{-2x}[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]\!}](../../4229480759610de8da772b0745c06b16b70b56ae.svg)
![{\displaystyle y''_{p}=e^{-2x}[sin(3x)(12Mx-6M-5Nx-4N)+cos(3x)(6N-5Mx-4M-12Nx)]\!}](../../57b163ea521277f918af0d523c1e8f0ca8e234ff.svg)
Plugging these into the ODE yields

![{\displaystyle 4[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]+}](../../2edffedd7a2b90e82102acd19a704b0b273dc2fd.svg)
![{\displaystyle 13x[Mcos(3x)+Nsin(3x)]=2cos(3x)\!}](../../d9655d1493f66fa3a0f7589a9c3631d9b4476def.svg)
Equating like terms allows us to solve for M and N
![{\displaystyle sin(3x)[(12Mx-6M-5Nx-4N)+4(N-2Nx-3Mx)+13Nx]=0\!}](../../a020f3dd194ee3d5cfeabb37b2da5e9f270c8290.svg)
![{\displaystyle cos(3x)[(6N-5Mx-4M-12Nx)+4(3Nx+M-2Mx)+13Mx]=2cos(3x)\!}](../../61f7febe8c0331fa45a5d99aafb6b7551136061a.svg)



So the particular solution is

Overall Solution
The overall solution in the sum of the homogeneous and particular solutions

![{\displaystyle y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)\!}](../../b9ba4455133d526b6750b7d4ad088a2b3ebeb60a.svg)
To find A and B we apply the initial conditions


Taking the derivative
![{\displaystyle y'(x)={\frac {d}{dx}}[e^{-2x}[cos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)]\!}](../../8363fdca8c2a01fd5519870363c110a30f746261.svg)
![{\displaystyle y'(x)=e^{-2x}[(3B+x-2)cos(3x)-(2B+{\frac {2}{3}}x+{\frac {8}{3}})sin(3x)]\!}](../../c86f7dc58a6220ae49af31a9fe4e261acfa83019.svg)


Giving us the overall solution
![{\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)+{\frac {1}{3}}xsin(3x)]\!}](../../c0df58d196d9072113ac3bbd23846cbeaa804059.svg)
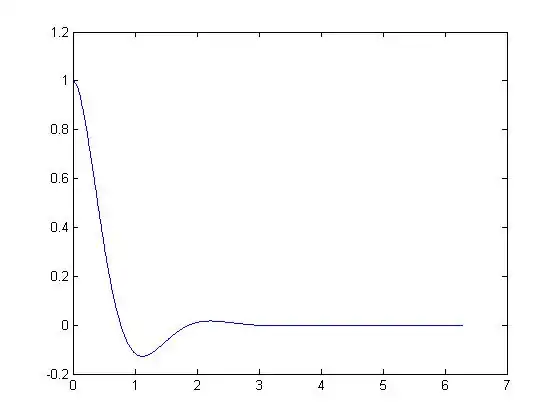
Plot
The period for  is
is 
Plotting the solution  over 3 periods yields
over 3 periods yields
R5.7
Solved by Daniel Suh
Problem Statement



1. Find the components  using the Gram matrix.
using the Gram matrix.
2. Verify the result by using  and
and  , and rely on the non-zero determinant matrix of
, and rely on the non-zero determinant matrix of  and
and  relative to the bases of
relative to the bases of  and
and  .
.
Part 1 Solution
Gram Matrix


Thus,




![{\displaystyle \Gamma =det[T]=(53)(11.25)-(24)(24)=20.25\!}](../../7a18e1ee1c3750d81d34b124c3b39230952ce917.svg)
Defining c
Define:


If  , then
, then  exists
exists

Finding c
 thus,
thus,  exists
exists



Part 2 Solution





 solution is correct
solution is correct
R5.8
Problem Statement
Find the integral
 for
for  and
and 
Using integration by parts, and then with the help of
General Binomial Theorem

Solution
For  :
:

For substitution by parts, 



Therefore:

Using the General Binomial Theorem:

Therefore:

Which we have previously found that answer as:

For  :
:

Initially we use the following substitutions: 

First let us consider the first term: 
Next, we use the integration by parts: 



Next let us consider the second term: 
Again, we will use integration by parts: 



Therefore:


Re-substituting for t:



Therefore:

Using the General Binomial Theorem for the integral with t substitution  :
:

Therefore:

Which we have previously found that answer as:

R5.9
Solved by: Gonzalo Perez
Problem Statement
Consider the L2-ODE-CC (5) p.7b-7 with  as excitation:
as excitation:
 (5) p.7b-7
(5) p.7b-7
 (1) p.7c-28
(1) p.7c-28
and the initial conditions
 .
.
Part 1
Part A
Project the excitation  on the polynomial basis
on the polynomial basis
 (1)
(1)
i.e., find  such that
such that
 (2)
(2)
for x in ![{\displaystyle [{\frac {-3}{4}},3]\!}](../../efbbc5a8b7f6494e546480187267b0e87c07e6fd.svg) , and for n = 3, 6, 9.
, and for n = 3, 6, 9.
Plot  and
and  to show uniform approximation and convergence.
to show uniform approximation and convergence.
Note that:
 (3)
(3)
Solution
To solve this problem, it is important to know that the scalar product is defined as the following:
 .
.
Therefore, it follows that:
 , where
, where  and
and  .
.
We know that if  are linearly independent, then by theorem on p.7c-37, the matrix is solvable.
are linearly independent, then by theorem on p.7c-37, the matrix is solvable.
According to this and (3)p.8-14:
If  exists
exists  . (3)p.8-14
. (3)p.8-14
Now let's define the Gram matrix  as a function of
as a function of  :
:
 (1)p.8-13
(1)p.8-13
Defining the "d" matrix as was done in (3)p.8-13, we get:
 . (3)p.8-13
. (3)p.8-13
And according to (1)p.8-15:  (1)p.8-15
(1)p.8-15
Now, we can find the values to compare  to
to  .
.
Using Matlab, this is the code that was used to produce the results:
The Matlab code above produced the following graph:
Where  is represented by the dashed line and the approximation,
is represented by the dashed line and the approximation, , is represented by the red line. This code can work for all n values.
, is represented by the red line. This code can work for all n values.
Part B
In a seperate series of plots, compare the approximation of the function  by Taylor series expansion about
by Taylor series expansion about  .
.
Where: 
Solution
For n=1:

For n=2:

For n=3:

For n=4:

For n=5:

For n=6:

For n=7:

For n=8:

For n=9:

For n=10:

For n=11:

For n=12:


For n=13:


For n=14:


For n=15:


For n=16:


Using Matlab to plot the graph:
Part 2
Find  such that:
such that:
 (1) p.7c-27
(1) p.7c-27
with the same initial conditions as in (2) p.7c-28.
Plot  for n = 3, 6, 9, for x in
for n = 3, 6, 9, for x in ![{\displaystyle [{\frac {-3}{4}},3]\!}](../../efbbc5a8b7f6494e546480187267b0e87c07e6fd.svg) .
.
In a series of separate plots, compare the results obtained with the projected excitation on polynomial basis to those with truncated Taylor series of the excitation. Plot also the numerical solution as a baseline for comparison.
Solution
First, we find the homogeneous solution to the ODE:
The characteristic equation is:


Then,

Therefore the homogeneous solution is:

Now to find the particulate solution
For n=3:


We can then use a matrix to organize the known coefficients:

Then, using MATLAB and the backlash operator we can solve for these unknowns:

Therefore

Superposing the homogeneous and particulate solution we get

Differentiating:
 Evaluating at the initial conditions:
Evaluating at the initial conditions:


We obtain:


Finally we have:

For n=6:


We can then use a matrix to organize the known coefficients:

Then, using MATLAB and the backlash operator we can solve for these unknowns:

Therefore

Superposing the homogeneous and particulate solution we get

Differentiating:
 Evaluating at the initial conditions:
Evaluating at the initial conditions:


We obtain:


Finally

For n=9:


We can then use a matrix to organize the known coefficients:


Then, using MATLAB and the backlash operator we can solve for these unknowns:

Therefore


Superposing the homogeneous and particulate solution we get


Differentiating:


Evaluating at the initial conditions:


We obtain:


Finally


Here is the graph for this problem using Matlab: