University of Florida/Egm4313/s12.team11.gooding/R2/2.1

Problem R2.1

Given the two roots and the initial conditions:

${\displaystyle \lambda _{1}=-2,\lambda _{2}=5\!}$
${\displaystyle y(0)=1,y'(0)=0\!}$

Find the non-homogeneous L2-ODE-CC in standard form and the solution in terms of the initial conditions and the general excitation ${\displaystyle r(x)\!}$.
Consider no excitation:
${\displaystyle r(x)=0\!}$
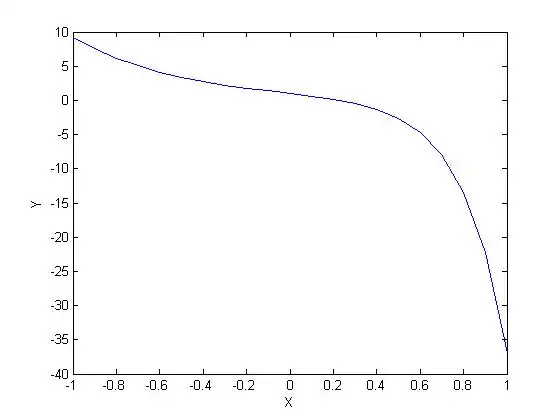
Plot the solution

${\displaystyle (\lambda -\lambda _{1})(\lambda -\lambda _{2})=0\!}$
${\displaystyle (\lambda +2)(\lambda -5)=\lambda ^{2}+2\lambda -5\lambda -10=0\!}$

 ${\displaystyle \lambda ^{2}-3\lambda -10=0\!}$

 ${\displaystyle y''-3y'-10=r(x)\!}$

${\displaystyle y_{h}(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}$
${\displaystyle y(x)=c_{1}e^{-2x}+c_{2}e^{5x}+y_{p}(x)\!}$
Since there is no excitation,
${\displaystyle y_{p}(x)=0\!}$

 ${\displaystyle y(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}$

${\displaystyle y(0)=1\!}$

 ${\displaystyle 1=c_{1}+c_{2}\!}$

${\displaystyle y'(0)=0\!}$

 ${\displaystyle 0=-2c_{1}+5c_{2}\!}$

Solving these two equations for ${\displaystyle c_{1}\!}$ and ${\displaystyle c_{2}\!}$ yields:

 ${\displaystyle c_{1}=5/4,c_{2}=-1/4\!}$

 ${\displaystyle y(x)=(5/4)e^{-2x}-(1/4)e^{5x}\!}$

Generate 3 non-standard (and non-homogeneous) L2-ODE-CC that admit the 2 values in (3a) p.3-7 as the 2 roots of the corresponding characteristic equation.

${\displaystyle 2(\lambda +2)(\lambda -5)=2\lambda ^{2}+4\lambda -10\lambda -20=0\!}$

 ${\displaystyle 2\lambda ^{2}-6\lambda -20=0\!}$

${\displaystyle 3(\lambda +2)(\lambda -5)=3\lambda ^{2}+6\lambda -15\lambda -30=0\!}$

 ${\displaystyle 3\lambda ^{2}-9\lambda -30=0\!}$

${\displaystyle 4(\lambda +2)(\lambda -5)=4\lambda ^{2}+8\lambda -20\lambda -40=0\!}$

 ${\displaystyle 4\lambda ^{2}-12\lambda -40=0\!}$

--Egm4313.s12.team11.gooding 02:01, 7 February 2012 (UTC)