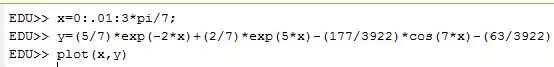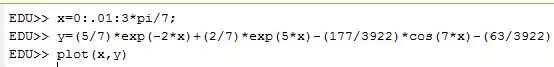Problem 5.5
Part 1
Problem Statement
Show that  and
and  are linearly independant using the Wronskian and the Gramain (integrate over 1 period)
are linearly independant using the Wronskian and the Gramain (integrate over 1 period)
Solution

One period of 
Wronskian of f and g

Plugging in values for 


![{\displaystyle =7[cos^{2}(7x)+sin^{2}(7x)]}](../../../b301de567d6ca791f8580ee8e9e260a31d103757.svg)
![{\displaystyle =7[1]}](../../../b92b8a5eea92d540f3a060ab9d154589aa005e48.svg)
They are linearly Independant using the Wronskian.







They are linearly Independent using the Gramain.
Problem Statement
Find 2 equations for the 2 unknowns M,N and solve for M,N.
Solution



Plugging these values into the equation given ( ) yields;
) yields;

Simplifying and the equating the coefficients relating sin and cos results in;


Solving for M and N results in;

Problem Statement
Find the overall solution  that corresponds to the initial conditions
that corresponds to the initial conditions  . Plot over three periods.
. Plot over three periods.
Solution
From before, one period  so therefore, three periods is
so therefore, three periods is 
Using the roots given in the notes  , the homogenous solution becomes;
, the homogenous solution becomes;

Using initial condtion  ;
;


with 

Solving for the constants;


Using the  found in the last part;
found in the last part;