Problem 1
Given
Find
Find the non-homogeneous L2-ODE-CC in standard form and the solution in terms of the initial conditions and the general excitation 
Consider no excitation:

|

|
Plot the solution.
Solution
Characteristic equation:

|

|
Substituting  into
into  :
:

|

|

|

|
Non-homogeneous solution:

|

|
Homogeneous solution:

|

|
Overall solution:

|

|
No excitation:

|

|
From intitial conditions:

|

|

|

|
Solving for  and
and  :
:

|

|
and

|

|
So, the final solution is:

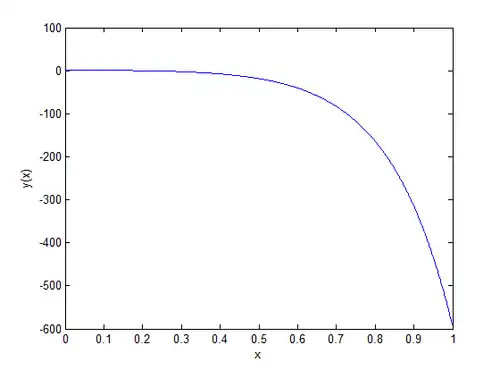
Problem 2
Given
Find
Find and plot the solution for 
Solution
Due to no excitation,  becomes:
becomes:

|

|
Substituting  into
into  :
:

|

|
Factoring, and solving for  :
:

|

|

|

|
Since  is a double root, the general solution:
is a double root, the general solution:

|

|
From intitial conditions:

|

|

|

|
Solving for  and
and  :
:

|

|
and

|

|
So, the final solution is:

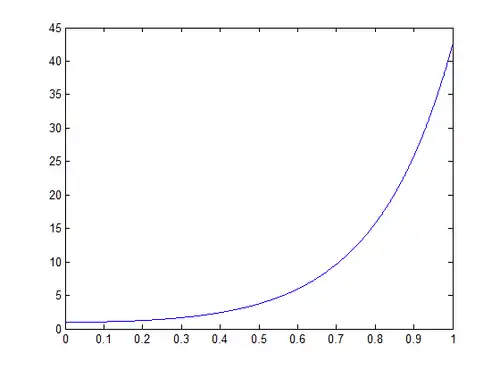
Problem 3
Given
(a)

(b)

Find
General solution to the differential equation
Solution
(a)
Characteristic equation:

Using the quadratic equation:

where:

Place values into quadratic equation:






(b)
Characteristic equation:

Using the quadratic equation:

where:

Place values into quadratic equation:





Problem 4
Given
(5)

|

|
(6)

|

|
h
Find
For both (5) and (6), find a general solution. Then, check answers by substitution.
Solution
(5)
To obtain the general solution for (Eq. 1), we let

This yields:

Therefore, we have:

Where  is a solution to the characteristic equation
is a solution to the characteristic equation

We can see that
 and
and .
.
Next, we must examine the quadratic formula to determine whether the system is over-, under-, or critically-damped.
The discriminant is:



Therefore, the equation is critically-damped.
The general solution is therefore represented by:

Where  .
.
We can determine the value of  by again using the quadratic equation, this time in full:
by again using the quadratic equation, this time in full:

for which we find that  .
.
Therefore, the general solution to the equation is:

Verification by substitution:


Plugging into Eq. 1 and combining terms, it is found:

All the terms cancel, so the statement is true, and the solution is verified.
(6)
To obtain the general solution for (Eq. 2), let

So then, we have

as a solution to the characteristic equation. All terms must be divided by 10, to put the equation in standard form:

Examining the discriminant, we find that

Therefore, the equation is critically-damped.
The general solution is represented by:

and  .
.
To determine the value of  , we set:
, we set:

for which we find that  .
.
Therefore, the general solution to the equation is:

Verification by substitution:


Plugging into Eq. 1 and combining terms, it is found:

All the terms cancel, so the statement is true, and the solution is verified.
Problem 5
Given

|
Given the basis:
(a)

|
(b)

|
Find
For the given Information above, Find an ODE for both (a) and (b)
Solution
(a)The general solution can be written as:

|
The characteristic equation can be written in the following way:

|
Giving the ODE:

|
(b) The general solution can be written as:

|
The characteristic equation can be written in the following way:

|
Giving the ODE:

|
Problem 6
Given
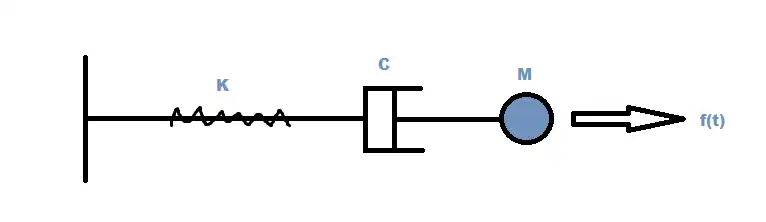 Mass Spring Dashpot system FBD's
Mass Spring Dashpot system FBD's
Spring-dashpot equation of motion from sec 1-5

|
Find
Spring-dashpot-mass system in series. Find the values for the parameters k,c,m with a double real root of 
Solution
Consider the double real root

|
Characteristic equation is

|

|
Recall

|

|
Thus

|

|

|
Solve for c

|
Therefore

Problem 7
Given
Taylor Series at t=0
Find
Develop the MacLaurin Series for 
Solution
Taylor series is defined as

|

|
The MacLaurin series occurs when t=0

|

|
Development of MacLaurin series for 

|

|
Final Answer

Explicit form can be written as

Development of MacLaurin series for 

|

|
Final Answer

Explicit form can be written as

Development of MacLaurin series for 

|

|
Final Answer

Explicit form can be written as

Problem 8
Given
(8)

|

|
(15)

|

|
Find
Solution
(8)
Assume that the solution is of the form

|

|

|

|
And

|

|
Substituting equations 2, 3, and 4 into equation 1a yields


Since


We must use the quadratic formula to obtain values for lambda





Where 

In order to verify solution, we must evaluate it's first and second derivative, then plug them into the equation
Let 


![{\displaystyle \displaystyle {y_{h}}'={C_{1}}[e^{ax}({jb}e^{jbx})+e^{jbx}({a}e^{ax})]+{C_{2}}[e^{ax}(-{jb}e^{jbx})+e^{jbx}({a}e^{ax})]}](../../eb5f9cabcf77cc9c2210361434cc7bea72cf5226.svg)
![{\displaystyle \displaystyle {y_{h}}''={C_{1}}[e^{ax}((jb)^{2}e^{jbx})+({jb}e^{jbx})({a}e^{ax})+e^{jbx}((a)^{2}e^{ax})+({a}e^{ax})({jb}e^{jbx})]+{C_{2}}[e^{ax}((jb)^{2}e^{-jbx})+(-{jb}e^{-jbx})({a}e^{ax})+e^{-jbx}((a)^{2}e^{ax})+({a}e^{ax})(-{jb}e^{-jbx})]}](../../42f644fe25767f357222289b191149d46895aae5.svg)
Plugging  into Eq. 1 and collecting terms gives
into Eq. 1 and collecting terms gives
![{\displaystyle \displaystyle 0={C_{1}}e^{ax}e^{jbx}[-b^{2}+jab+a^{2}+jab+jb+a+3.25]+{C_{2}}e^{ax}e^{-jbx}[-b^{2}-jab+a^{2}-jab-jb+a+3.25]}](../../6292050c6caf4604fa3b5dbbb4e8238d9f226a5f.svg)
![{\displaystyle \displaystyle 0={C_{1}}e^{-0.5x}e^{j{{\sqrt {3}}x}}[-3-j{\sqrt {3}}/2+1/4-j{\sqrt {3}}/2+j{\sqrt {3}}-1/2+3.25]+{C_{2}}e^{-0.5x}e^{-j{\sqrt {3}}x}[-3+j{\sqrt {3}}/2+1/4+j{\sqrt {3}}/2-j{\sqrt {3}}-1/2+3.25]}](../../b233836a6ecfc07a1d38a3407fe5a3bdaa1019c3.svg)

Therefore the solution holds for any values of 
(15)
Assume that the solution is of the form

|

|

|

|
And

|

|
Substituting equations 2, 3, and 4 into equation 1b yields


Since


We must use the quadratic formula to obtain values for lambda




Where 

In order to verify solution, we must evaluate it's first and second derivative, then plug them into the equation
Let 


![{\displaystyle \displaystyle {y_{h}}'={C_{1}}[e^{ax}({jb}e^{jbx})+e^{jbx}({a}e^{ax})]+{C_{2}}[e^{ax}(-{jb}e^{jbx})+e^{jbx}({a}e^{ax})]}](../../eb5f9cabcf77cc9c2210361434cc7bea72cf5226.svg)
![{\displaystyle \displaystyle {y_{h}}''={C_{1}}[e^{ax}((jb)^{2}e^{jbx})+({jb}e^{jbx})({a}e^{ax})+e^{jbx}((a)^{2}e^{ax})+({a}e^{ax})({jb}e^{jbx})]+{C_{2}}[e^{ax}((jb)^{2}e^{-jbx})+(-{jb}e^{-jbx})({a}e^{ax})+e^{-jbx}((a)^{2}e^{ax})+({a}e^{ax})(-{jb}e^{-jbx})]}](../../42f644fe25767f357222289b191149d46895aae5.svg)
Plugging  into Eq. 1 and collecting terms gives
into Eq. 1 and collecting terms gives
![{\displaystyle \displaystyle 0={C_{1}}e^{ax}e^{jbx}[-b^{2}+jab+a^{2}+jab+(0.54)(jb+a)+0.0729+\pi ]+{C_{2}}e^{ax}e^{-jbx}[-b^{2}-jab+a^{2}-jab+(0.54)(-jb+a)+0.0729+\pi ]}](../../b13805e189cce9de3a85ed19606ed883b11a2531.svg)
![{\displaystyle \displaystyle 0={C_{1}}e^{-0.27x}e^{j{1.772x}}[-(1.772)^{2}+j(-0.27)(1.772)+(0.27)^{2}+j(-0.27)(1.772)+(0.54)(j(1.772)-0.27)+0.0729+\pi ]+{C_{2}}e^{-0.27x}e^{-j1.772x}[-(1.772)^{2}-j(-0.27)(1.772)+(0.27)^{2}-j(-0.27)(1.772)+(0.54)(-j(1.772)-0.27)+0.0729+\pi ]}](../../42085b728ca2c11f524a1f023c248f8f1442fd4f.svg)

Therefore the solution holds for any values of 
Problem 9
Given
Find
Solution
Problem 10
Given
Differential equation, initial conditions, and forcing function as shown:

|

|

|

|
Find
Find
The solution to Eq. 1
Solution

|

|

|

|

|

|
Substituting Equations 2, 3, and 4 into Equation 1 yields

|

|
To solve for the constants:

|

|

|

|

|

|

|

|
Solving Equations 6-9 yields

|

|
The homogeneous solution:

|

|
The total solution:

|

|
Setting  yields
yields

|

|
Solving for  yields
yields

|

|
Finding  yields
yields

|

|
Setting  yields
yields

|

|
Solving for  yields
yields

|

|
Therefore, the total solution is

|

|
Team Member Tasks
| Name |
Responsibilities |
Checked by
|
| Bo Turano |
Problem R2. |
--
|
| David Parsons |
Problem R2.4 |
--
|
| Dean Pickett |
Problem R2.8 |
--
|
| Giacomo Savardi |
Problem R2. |
--
|
| Isaac Kimiagarov |
Problem R2.3 |
--
|
| Kyle Steiner |
Problem R2. |
--
|
| Tony Han |
Problem R2.6, R2.7 |
--
|
All team members contributed to the coding of this page.


